Average power dissipation for induced current

[auctor]

Homework Statement

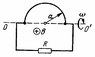
A wire shaped as a semi-circle of radius a rotates about the axis OO’ with a constant angular velocity ω in a uniform magnetic field with induction B (attached figure). The plane of the rectangular loop is perpendicular to the magnetic field direction. The total resistance of the circuit is R. Neglecting effects of the magnetic field that is generated by the current in the circuit, find the mean thermal power dissipated during one rotation period.

Homework Equations

Emf: ε=-dΦ/dt
Flux: dΦ=B⋅dS
Angle: ϑ=ωt
Current: I=ε/R
Power: P=εI
∫₀^2π sin²(x)dx = 1/2

The Attempt at a Solution

The area of the projection of the loop onto the direction perpendicular to the magnetic field changes according to S=S_rectangle+πa²/2 cos(ϑ)=S_rectangle+πa²/2 cos(ωt)
The magnetic induction isn't changing.
The flux as a function of time is then Φ=B(S_rectangle+πa²/2 cos(ωt))
The emf is ε=-dΦ/dt = ωBπa²/2 sin(ωt)
The current is I=ωBπa²/(2R) sin(ωt)
The instantaneous power is P=[ωBπa²]²/(4R) sin²(ωt)
The average power is P=[ωBπa²]²/(8R)

However, the answer the book gives is P=[ωBπa²]²/(2R). This result would correspond to a variation of the projection area S=S_rectangle+πa² cos(ϑ). Not sure why this would be the case...

 

[TSny]

Your work looks correct to me. I agree with your result for the average power.

(Your expression for the instantaneous power is missing a square on the sine function.)

 

[auctor]

Thanks! (Square for sine corrected.) Just wondered if the book has a typo or if I was missing some subtlety.