CynicusRex
Gold Member
- 98
- 68
Am I forgetting some critical basic knowledge?
It says: In the plane (identified by R^2) a linear equation ax+by=c is a straight line. If b=0 then this straight line is parallel with the y-axis; in the other case it is a straight line with slope -a/b. A (2 by 2)-system linear equation.
Why is it parallel? If you make b=0 in ax+by=c you still get a straight line. Or should I see it as: b y = -ax + c

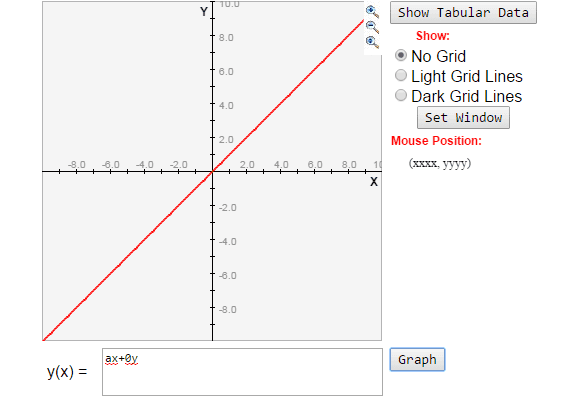
It says: In the plane (identified by R^2) a linear equation ax+by=c is a straight line. If b=0 then this straight line is parallel with the y-axis; in the other case it is a straight line with slope -a/b. A (2 by 2)-system linear equation.
Why is it parallel? If you make b=0 in ax+by=c you still get a straight line. Or should I see it as: b y = -ax + c
Last edited: