Balancing 3 Forces - Finding Ta & Tb

[Electro]

Hello Everyone,

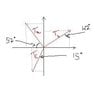
I solved an exercise that has to do with equilibrium. There are 3 forces and I should find the tensions Ta and Tb in the 2 cords. (I drew a simple picture so that it would be more clear to you). I solved the exercise following physical principles (I think I did it correct) but I get negative values for Ta and Tb.

The equations I derived are:
Tb*sin(42) - Ta*cos(57)-Tc*sin(15)=0 For X
Tb*cos(42)+Ta*sin(57)-Tc*cos(15)=0 For Y

But still I get the negative values. What might be wrong?

 

[Diane_]

I can't see your diagram yet - it hasn't been approved - so I can't really comment specifically. In general, though, remember that tensions are forces, i.e. they're vectors. The negative sign could be an error, of course, but it could also simply indicate that the directions you originally assigned to those tensions were backwards - in other words, the forces are pulling opposite to the direction you thought. You might look at the problem and see if that makes any sense. I'll try to check back when the diagram is available.

 

[Electro]

Thanks a lot,
I hope you will see the diagram ASAP because the project I have due is on Thursday. The equations I set up, are reasonable but there's a "?" that I don't understand.
THanx

 

[Diane_]

I apologize if this is too late, but today is the first day I've been able to see the diagram.

I get the same two equations you do, so I don't think the problem is there. In setting them up as you (and I) did, the directions are implicitly taken care of in the signs given to the various terms.

The only problem left is that the problem is insoluable as it stands. You have three unknowns, but only two equations. Physically, this corresponds to saying "you're going to pull on three different ropes in three specific directions. How hard do you have to pull in order not to move?" The response is, "it depends on how hard you pull on any of them." A simple, trivial solution would be to make the tensions in all three ropes zero. This is probably not what your teacher had in mind. If you know the tension in anyone of the ropes, you can find the other two. As it stands, though, all you can say is how the three relate to each other.

In mathematics terms: two equations in three unknowns admits to an infinite number of solutions.

Again, sorry this didn't come quicker.