Basic Proportionality Theorem (Thales Theorem)

[SSG-E]

Homework Statement

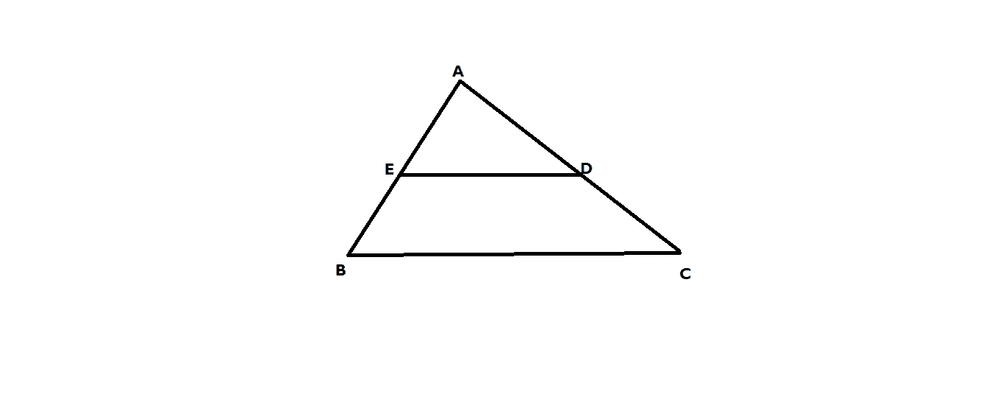
If ED is parallel to BC then prove that:
(1). AB/EB = AC/DC
(2). AB/AE = AC/AD

Relevant Equations

AB/EB = AC/DC
AB/AE = AC/AD

According to Basic proportionalit theorem
if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides proportionaly.
I can't figure a way out how to prove it.
Here is an attempt.
we know that AE/EB = AD/DC.

 

[BvU]

Here is an attempt.
we know that AE/EB = AD/DC.

It's what we have to prove ! How do "we know that ... " !

 

[SSG-E]

It's what we have to prove ! How do "we know that ... " !

Actually we have to prove the corollary AB/EB = AC/DC not AE/EB = AD/DC.

 

[BvU]

What do you know about similar triangles ?

 

[SSG-E]

What do you know about similar triangles ?

The ratio of their corresponding sides is equal.

 

[SSG-E]

What do you know about similar triangles ?

?

 

[Delta2]

Bring the parallel line to AC from the point E that intersects BC at point F. Then because EFCD is a parallelogram you ll have that EF=CD. Also use the fact that all 3 triangles ABC,AED and EBF are similar. I think having those in mind you should be able to prove 1 and 2.

 

[SSG-E]

Bring the parallel line to AC from the point E that intersects BC at point F. Then because EFCD is a parallelogram you ll have that EF=CD. Also use the fact that all 3 triangles ABC,AED and EBF are similar. I think having those in mind you should be able to prove 1 and 2.

No didn't get it.

 

[Delta2]

What do you get from the similarity of triangles ABC and EBF?

 

[SSG-E]

What do you get from the similarity of triangles ABC and EBF?

No didn't get it

 

[SSG-E]

What do you get from the similarity of triangles ABC and EBF?

The correponding sides are porportional

 

[Delta2]

Yes but can you write the specific equation involving sides AB EB AC and EF?

 

[SSG-E]

Yes but can you write the specific equation involving sides AB EB AC and EF?

AB/EB = AC/EF =1

 

[Delta2]

Almost correct, you have to remove the =1 part. Now as I told earlier we know that EF=DC (because EFDC is a parallelogram). So what do you get afterall?

 

[SSG-E]

Almost correct, you have to remove the =1 part. Now as I told earlier we know that EF=DC (because EFDC is a parallelogram). So what do you get afterall?

AB/EB = AC/DC

 

[SSG-E]

AB/EB = AC/DC

It was taht simple?

 

[Delta2]

Yes, it just needed a bit of imagination to bring that parallel line from E to side AC.
Now to prove (2) work with the similarity on triangles ABC and AED. No need to bring any parallel line for this proof.

 

[SSG-E]

Yes, it just needed a bit of imagination to bring that parallel line from E to side AC.
Now to prove (2) work with the similarity on triangles ABC and AED. No need to bring any parallel line for this proof.

AB/EB = AC/DC = K
AB/AE = AB/AB-EB = AB/AB - AB/EB = 1-K ...a
AC/AD = AC/AC-DC = AC/AC - AC/DC = 1...b
Thus, AB/AE = AC/AD (from 'a' and 'b')

figured it out after an hour, is it correct

 

[Delta2]

Well no the algebra for the equalities of line 2 and 3 is not completely correct because for example $$\frac{AB}{AB-EB}\neq \frac{AB}{AB}-\frac{AB}{EB}$$. But it is $$\frac{AB-EB}{AB}=\frac{AB}{AB}-\frac{EB}{AB}$$ so work with the ratio of $$\frac{AE}{AB}$$ and $$\frac{AD}{AC}$$ instead and you ll be able to prove it in the same spirit, that is using (1) and algebra. However the way I originally proposed at post #17 with similarity of triangles ABC and AED, gives the result in a simple step, without algebraic manipulation.