- #1
grimTesseract
- 4
- 0
Homework Statement
OK, I am new to these kinds of problems and I am trying to learn the appropriate properties but they are proving somewhat difficult for me... I hope I am going in the right direction.
Homework Equations
[/B]
The first problem corresponds to the figure with 'Rep' in the filename. I need merely to measure the angle 'a.' I'm a little stuck because, given the angle 105 degrees, I was under the impression that the angles of the opposite vertices of the triangle must sum 105, and that the adjacent angle must be 180 - 105 = 75, but in the diagram on my worksheet the triangle looks equilateral.
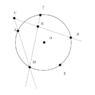
The second problem will correspond to the uploaded figure with 'exam' in the filename.
Given a circumference with center ##O##, radius ##r## and diameter ##AB##, we consider the point ##E##, in the arc ##AB## given the figure. Let ##M## be a variable point on the arc ##AE##, and on the line containing the segment ##MA## let ##C## be the point such that ##MC = MB##. ##MF## is the perpendicular line to ##CB## through ##M##, ##F## being the intersection of the line and the circumference. ##MF \cap CB = {H}##
a) Classify the triangle MBC by its sides and angles.
b) Prove that the angle FMB is constant when varying M, and thus that F is a fixed point.
c) What geometric figure is included in the locus of the point H when M varies? (CHM = 90 degrees)
d) Prove that the triangles BHO and BCA are similar
e) Utilizing parts (c) and (d), deduce the geometric figure included in the locus of C.
I am significantly more lost here. (c) and logically (e) confound me and I'm not sure how to go about solving them. I can't tell how to deduce the angles of MBC but I would say it's isosceles, given that I'm told ##MC = MB##. Proving the part (b) seems like it must somehow relate to the central angle, but I don't see exactly how I must prove this. Finally, I can see that BHO is a scaled down version of BCA, but I don't know how to prove the similarity in angles.
All help is appreciated here.