Basic RC Circuit Homework: Calculate Time Constant & Charge Decay

[STEMucator]

Homework Statement

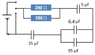
The emf of the battery in the given circuit is $\epsilon = 8.0 V$.

(a) Calculate the time constant of the circuit.
(b) Calculate the charge in Coulombs when the capacitor is fully charged.

(c) If the effective capacitor is allowed to discharge through the effective resistance, show that the expression for the time taken for half of the initial charge to decay away is:

$$T_{Half} = (RC) ln(2)$$​

(d) Calculate this time.
(e) Calculate the initial current in $mA$, just as the effective capacitor starts to discharge and assume that is was fully charged by the battery.

Homework Equations

$\epsilon = 8.0 V$
$R_1 = R_2 = 390 \Omega$
$C_1 = 5 \mu F = 5 \times 10^{-6} F$
$C_2 = 6.4 \mu F = 6.4 \times 10^{-6} F$
$C_3 = 95 \mu F = 95 \times 10^{-6} F$
$C_4 = 35 \mu F = 35 \times 10^{-6} F$

The Attempt at a Solution

(a) I believe they are referring to the RC time constant. So it would probably be convenient to find an equivalent resistance and capacitance for the circuit.

$R_{eq} = (\frac{1}{R_1} + \frac{1}{R_2})^{-1} = (\frac{1}{390 \Omega} + \frac{1}{390 \Omega})^{-1} = 195 \Omega$

$C_{eq} = (\frac{1}{C_1} + \frac{1}{C_2 + C_3} + \frac{1}{C_4})^{-1} = (\frac{1}{5 \times 10^{-6} F} + \frac{1}{(6.4 + 95)\times 10^{-6} F} + \frac{1}{35 \times 10^{-6} F})^{-1} = 4.194 \times 10^{-6} F = 4.2 \times 10^{-6} F$

Therefore the time constant is $\tau = R_{eq}C_{eq} = (195 \Omega)(4.194 \times 10^{-6} F) = 8.178 \times 10^{-4} s = 8.2 \times 10^{-4} s$.

(b) Suppose the top switch is closed completing the circuit. To find the charge when the capacitor is fully charged, note that the potential difference of the capacitor will be equal to the emf of the ideal battery at this time:

$q_{eq} = C_{eq}V_{eq} = C_{eq} \epsilon = (4.194 \times 10^{-6} F)(8.0 V) = 3.355 \times 10^{-5} C = 3.4 \times 10^{-5} C$

(c) Suppose the bottom switch is now closed instead. While a capacitor is discharging, the charge decreases with time according to $q(t) = q_0e^{- \frac{t}{RC}}$ where $q_0 = q_{eq}$. Note that half of the initial charge is $\frac{q_{eq}}{2}$. So we obtain:

$q(t) = q_0e^{- \frac{t}{RC}}$
$\frac{q_{eq}}{2} = q_{eq}e^{- \frac{T_{Half}}{RC}}$
$\frac{1}{2} = e^{- \frac{T_{Half}}{RC}}$
$\ln(\frac{1}{2}) = - \frac{T_{Half}}{RC}$
$- \ln(2) = - \frac{T_{Half}}{RC}$
$T_{Half} = RC \ln(2)$​

(d) Calculating the time we obtain:

$T_{Half} = RC \ln(2) = R_{eq}C_{eq} \ln(2) = (195 \Omega)(4.194 \times 10^{-6} F) \ln(2) = 5.669 \times 10^{-4} s = 5.7 \times 10^{-4} s$

(e)

Taking the time derivative of $q(t) = q_0e^{- \frac{t}{RC}}$, we obtain the current $i(t) = -(\frac{q_0}{RC}) e^{- \frac{t}{RC}}$. The initial current is given at $t =0$:

$i(0) = -(\frac{q_0}{RC}) = -\frac{3.355 \times 10^{-5} C}{(195 \Omega)(4.194 \times 10^{-6} F)} = - 0.041 A = - 41 mA$

Where the negative sign indicates the charge is decreasing. Therefore, the initial current before discharge was $41 mA$.

Do these look okay? I hope I haven't done anything wrong.

 

[NascentOxygen]

Is there a schematic to go with this?

 

[STEMucator]

Is there a schematic to go with this?

Yes I thought I had uploaded it before, here it is now:

 

[gneill]

Do these look okay? I hope I haven't done anything wrong.

Your calculations and results look fine.

Note that for part (e) you could have simply noted that at the initial instant the capacitance had a voltage across it of 8.0 V, and that's impressed across the resistance R = 195 Ω. Then use Ohm's law to find the current at that instant.