Bead sliding along wire with constant horizontal velocity -- Shape of wire?

[zenterix]

Homework Statement

The following is exercise 5 from Chapter 4 of Morin's Introduction to Classical Mechanics. There is no solution in the book for these "Exercises", only for "Problems".

A bead, under the influence of gravity, slides along a frictionless wire whose height is given by the function $y(x)$. Assume that at position $(x, y) = (0, 0)$, the wire is horizontal and the bead passes this point with a given speed $v_0$ to the right. What should the shape of the wire be (that is, what is y as a function of $x$) so that the horizontal speed remains $v_0$ at all times? One solution is simply $y = 0$. Find the other.

There is a footnote:

Solve this exercise in the spirit of Problem 6, that is, by solving a differential equation. Once you get the answer, you’ll see that you could have just written it down without any calculations, based on your knowledge of a certain kind of physical motion.

Relevant Equations

$F=ma$

We start with something like

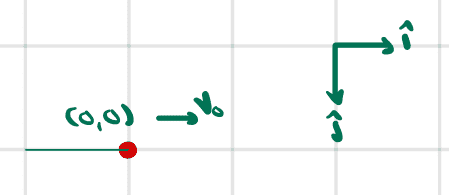
If we suppose the wire is the green line, we are to figure out what the green line looks like to the right of the red bead.

What I first thought of was simply

$$\vec{r}'(t)=x'(t)\hat{i}+y'(t)\hat{j}=v_0\hat{i}+gt\hat{j}\tag{1}$$

$$\vec{r}(t)=x(t)\hat{i}+y(t)\hat{j}=v_0t\hat{i}+\frac{gt^2}{2}\hat{j}\tag{2}$$

Thus, $\vec{r}(t)$ represents the position of the wire.

Then I wanted to solve the problem in a way that would also give me the solution with $y(t)=0$ (and $x(t)=v_0t$).

The initial solution above assumes there is no normal force at all on the bead from the wire.

If there were a normal force, we'd have

$$mg\hat{j}-\vec{N}=m\vec{a}\tag{3}$$

$$mg\hat{j}-(mg\cos{\alpha}\sin{\alpha}\hat{i}-mg\cos^2{\alpha})=ma_y\hat{j}\tag{4}$$

$$\implies mg\cos{\alpha}\sin{\alpha}=0\tag{5}$$

$$\implies \alpha = 0\ \text{or}\ \frac{\pi}{2}\tag{6}$$

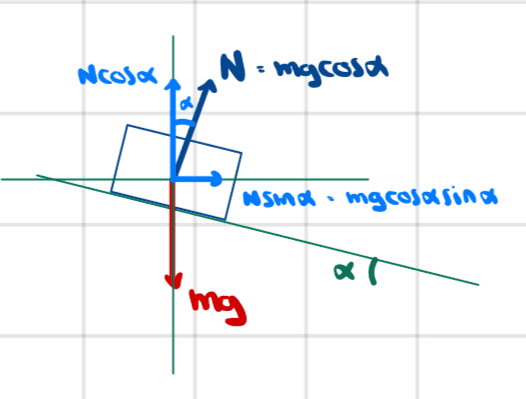
Note that I am defining alpha as follows

If $\alpha=\frac{\pi}{2}$ then the normal force is zero altogether, $mg\hat{j}=ma_y\hat{j}$, and thus $a_y=g$. There are no forces in the horizontal direction thus no acceleration either.

It seems we can write (1) and go from there.

If $\alpha=0$ then $\vec{N}=-mg\hat{j}$ and the 2nd law becomes $0\hat{j}=ma_y\hat{j}\implies a_y=0$.

Thus, $\vec{r}'(t)=v_0\hat{i}$ and $\vec{r}(t)=v_0t\hat{i}$. Thus, in this case, $y(t)=0$.

My question is if this approach is the one mentioned by the footnote. Is the "differential equation" mentioned there simply the equations involving $\vec{r}'(t)$ that I have used, or is there some other way?

 

[pasmith]

We can't tell you if that approach is "in the spirit of problem 6" if you don't tell us what problem 6 is; not everyone has access to a copy of your text.

Since the position is contrained to be $(x, f(x))$ so that the velocity is $(\dot x, f'(x) \dot x)$ I would start with the Lagrangian $$L(x, \dot x) = \tfrac12 m(1 + f'(x)^2)\dot x ^2 - mgf(x)$$ and obtain the Euler-Lagrange equation. Then the condition that $\dot x = v_0$ is constant requires $\ddot x = 0$. What is left is a differential equation for $f$ subject to $f(0) = f'(0) = 0$.

EDIT: The other approach, which I think is what you have attempted, is to set $\theta$ as the angle between the tangent to the wire and the horizontal so that $\tan \theta = f'(x)$, and $N$ as the magnitude of the normal reaction force; then the horizontal and vertical components of Newton II are $$\begin{split} m\ddot x &= N \sin \theta \\ m \ddot y &= N \cos \theta - mg. \end{split}$$ Now $$\begin{split} N \cos \theta \tan \theta &= N \sin \theta \\ (\ddot y+ g)f'(x) &= \ddot x\end{split}$$ is where you want to start from.

 

[zenterix]

@pasmith I was confused about which problem was being referred to but now I can see it is the following

A bead, under the influence of gravity, slides along a frictionless wire whose height is given by the function $y(x)$. Assume that at position $(x, y) = (0, 0)$ the wire is vertical and the bead passes this point with a given speed $v_0$ downward. What should the shape of the wire be (that is, what is $y$ as a function of $x$) so that the vertical speed remains $v_0$ at all times?

This problem does have a solution in the book.

So at this point I think I can see the approach that was intended.