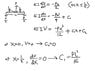Discussion Overview
The discussion revolves around calculating beam deflection at specific points (x=L/4 and x=L/2) and understanding the boundary conditions related to the slope of the beam. It includes theoretical considerations and interpretations of physical meanings behind the mathematical expressions involved.
Discussion Character
- Homework-related
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant states that the displacement at x=0 is zero, leading to a constant C2=0, but expresses uncertainty about the boundary conditions.
- Another participant explains that the slope of the beam is represented by dv/dx.
- A participant questions the physical meaning of the slope and its value at x=L/2, suggesting that it should not be zero due to the presence of an upward load P.
- There is a discussion about the relationship between the derivative of moment, shear force, and distributed force, with a participant noting that this may not directly relate to deflection.
- One participant emphasizes the need to start with deflection and questions the interpretation of the first derivative of a curve.
- Another participant reiterates the definition of slope in calculus but does not resolve the disagreement about its value at x=L/2.
Areas of Agreement / Disagreement
Participants express differing views on the value of dv/dx at x=L/2, with some asserting it should be zero while others argue that it cannot be zero due to the applied load. The discussion remains unresolved regarding the boundary conditions and their implications.
Contextual Notes
There are uncertainties regarding the physical interpretation of slope and its implications for beam deflection, as well as the assumptions underlying the boundary conditions used in the calculations.