Beta/gamma decay probabilities

[CloudNine]

Hi all,

I have received this following question which I can't really figure out all the way to the end:

Consider the beta decay of 212Pb:

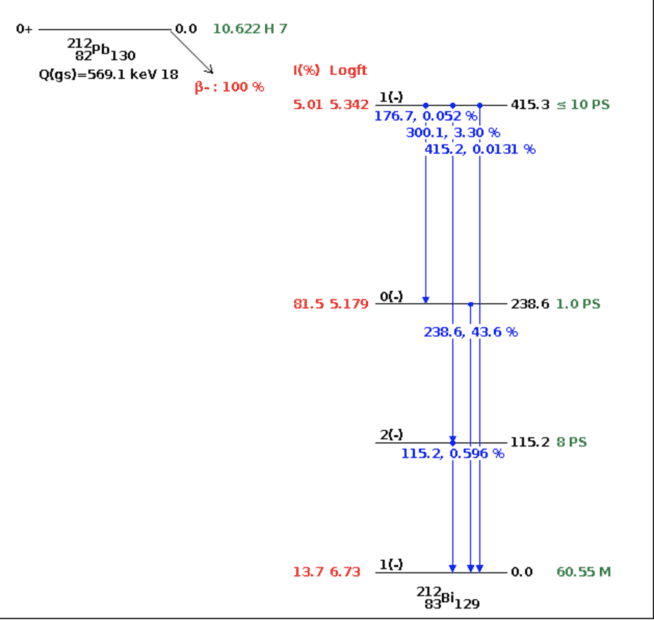
* What is the probability that the decay leads to the second excited state of 212Bi at 238.6 keV?
This is straight forward - from nndc NuDat, it seems that the answer is simply 81.5%:

*What is the probability that the beta decay is accompanied by the emission of a 238.6 keV gamma ray? Explain (qualitatively) the difference between this value and your answer to (a).
Here, the answer is, if I'm not mistaken (but here's my difficulty) is like so:
Lets define:
A - beta decay to the second excited state of Bi-212
B - gamma decay with 238.6 KeV
Since decaying with 238.6 KeV can only happen from the 2nd excited state of Bi-212, the events are dependent. Thus:
P(B∩A)=P(B|A)P(A)=0.436*0.815=0.35534
I don't understand "what is the difference" between this value and the answer to (a). These are different questions, depicting different situations..

*Google the binding energies of the bismuth K, L, M and N shells. Use this information and the Nudat database to identify the main emissions which solve the mystery of (b).
Totally lost it! What mystery? :( Is this the correct table to use? What does it give?

 

[mfb]

I think the problem asks indirectly how the other 56% of the nuclei go to the ground state if they don't emit a gamma photon.

 

[CloudNine]

I think the problem asks indirectly how the other 56% of the nuclei go to the ground state if they don't emit a gamma photon.

Yes I think you are right. I've dived into the theoretical explanations again and things make more sense now, and so I'm able to compile a coherent answer (hopefully).
Thanks!