Bilinear transformation not working

[Sneaky6666]

I want to try this bilinear transformation of a rectangle to a quad described here
http://www.fmwconcepts.com/imagemagick/bilinearwarp/FourCornerImageWarp2.pdf
on page 4.

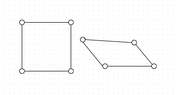
I have the square

$$(500,900)(599,900)(599,999)(500,999)$$

and the quad

$$(454,945)(558,951)(598,999)(499,999)$$

It looks like this

Bilinear transformation not working-capture.png

Where the ith entry of the quad and square coordinates above are corresponding corners.

With that in place, I can make the following matrices

$$\begin{bmatrix} 1 & 500 & 900 & 450000 \\ 1 & 599 & 900 & 539100 \\ 1 & 599 & 999 & 598401 \\ 1 & 500 & 999 & 499500 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} 454 \\ 558 \\ 598 \\ 499 \end{bmatrix}$$

$$\begin{bmatrix} 1 & 500 & 900 & 450000 \\ 1 & 599 & 900 & 539100 \\ 1 & 599 & 999 & 598401 \\ 1 & 500 & 999 & 499500 \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} 945 \\ 951 \\ 999 \\ 999 \end{bmatrix}$$

If I solve for them I get

$$a0=-709.911845730028$$
$$a1=1.50964187327824$$
$$a2=0.709621467197225$$
$$a3=-0.000510152025303541$$
$$b0=148.305785123967$$
$$b1=0.611570247933884$$
$$b2=0.85154576063667$$
$$b3=-0.000612182430364249$$

But then when I run this python script (I want to simulate manually, converting the point (454, 945) on the quad to the point (500,900) on the square), I get a different answer. I get (442.90822654, 1024.0)...

    X = 454
    Y = 945
    
    a0=-709.911845730028
    a1=1.50964187327824
    a2=0.709621467197225
    a3=-0.000510152025303541
    
    
    b0=148.305785123967 
    b1=0.611570247933884 
    b2=0.85154576063667 
    b3=-0.000612182430364249
    
    A = b2*a3 - b3*a2
    C_one = (b0*a1 - b1*a0)
    C = C_one + (b1*X - a1*Y)
    B_one = (b0*a3 - b3*a0) + (b2*a1 - b1*a2)
    B = B_one + (b3*X - a3*Y)
    
    V = (-B + (B*B - 4*A*C)**0.5 ) / (2*A)
    U = (X - a0 - a2*V) / (a1 + a3*V)
    
    print U,V

Does anyone know what's wrong?

Thanks

 

[Ackbach]

Hmm, interesting. The bilinear transformation code seems correct to me. I noticed, though, that there appears to be a .jpg file concerning your original matrices where you compute the $a_0, a_1,$ etc, that didn't load. Could you please give some background on how you constructed those matrices?

Incidentally, wanting to check your four "cardinal" points is a very good idea! Sanity checks in general are essential.

[EDIT] For reference, when I copy your code to Mathematica (really Wolfram Programming Cloud), I get the same result you do. So I don't think you're getting any weird sort of round-off or numerical error here.

 

[Sneaky6666]

I added the missing image above. And the matrix is based off the pdf file on page 4.

X = a0 + a1U + a2V + a3UV
Y = b0 + b1U + b2V + b3UV

Where X, and Y is coordinates on the quad, and U,V and coordinates on the square. By substituting the 4 pairs of corresponding corner coordinates, I get 8 equations. But a and b coefficients are independent, so I can separate it into 2 systems of equations of 4 unknowns.

 

[Sneaky6666]

I did a test and tried to warp an image and this seems to work in general, but then in two places the formula messed up. See these two pics.

The left eye got messed and the right leg got messed too. The above example quad is for the right leg.

original:
View attachment 4605

warped:
View attachment 4606

using this warp template:
View attachment 4607

 

[Sneaky6666]

I was able to fix it, using three methods. The issue was numerical unstability in the quadratic function to calculate the y coordinate.

1. Use the much more stable quadratic formula
http://www.it.uom.gr/teaching/linearalgebra/NumericalRecipiesInC/c5-6.pdf

2. translate the square to location 0,0.

3. Scale the square into a unit square.

------

3. helped a bit, 2. not sure if it made a difference, and 1. was a huge boost in accuracy.

 

[Ackbach]

I was able to fix it, using three methods. The issue was numerical unstability in the quadratic function to calculate the y coordinate.

1. Use the much more stable quadratic formula
http://www.it.uom.gr/teaching/linearalgebra/NumericalRecipiesInC/c5-6.pdf

3. translate the square to location 0,0.

2. Scale the square into a unit square.

------

3. helped a bit, 2. not sure if it made a difference, and 1. was a huge boost in accuracy.

Excellent! I'm glad you found something that worked out, and thanks so much for posting it here for our edification. You learn something new every day. I had no idea that the regular quadratic can be numerically unstable. It makes sense given the explanation - subtraction is usually the culprit.