Block floating in between oil and water, what's the FBD?

[danjordan]

[Mentor note: This thread was moved from General Physics due to it being homework related]

A friend and I were reviewing problems from a GRE subject which read:
"A layer of oil with density 800 kg/m^3 floats on top of a volume of water with density 1000 kg/m^3. A block floats at the oil-water interface with 1/4 of its volume in oil and 3/4 of its volume in water, as shown in the figure above (below; i found a similar image). What is the density of the block?"

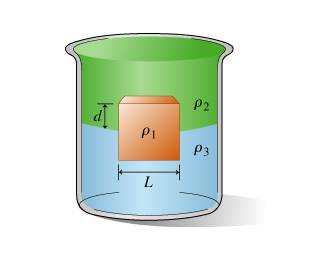
I solved it using the formula for the buoyant force, F = ρVg and the weight. So the balance was:
800gV/4 + 1000g*3V/4 = ρVg
950 kg/m^3 = ρ
In this I considered both buoyant forces, from oil and water to be directed upwards.

However, my friend considered the pressure at the depth of the top of the block to be P0, and at the bottom of the block to be P1. So (being 4h the height of the block, and A its top & bottom area):
P1 = P0 + ρ_oil*h*g + ρ_water*3h*g
When I work out the forces on the block (the weight of the oil above, the pressure on the bottom of the block) I'd get a balance:
P1*A = W + P0*A
Replacing the values we got the same value of density, 950 kg/m^3.

What is breaking my brain is the fact that I considered the buoyant force of the oil on the block to be upwards, while my friend considered it to be downwards on the block.

I want to know what is the real free-body diagram for the block and is the oil pushing down on the block or pulling it up?

 

[SteamKing]

A friend and I were reviewing problems from a GRE subject which read:
"A layer of oil with density 800 kg/m^3 floats on top of a volume of water with density 1000 kg/m^3. A block floats at the oil-water interface with 1/4 of its volume in oil and 3/4 of its volume in water, as shown in the figure above (below; i found a similar image). What is the density of the block?"

I solved it using the formula for the buoyant force, F = ρVg and the weight. So the balance was:
800gV/4 + 1000g*3V/4 = ρVg
950 kg/m^3 = ρ
In this I considered both buoyant forces, from oil and water to be directed upwards.

However, my friend considered the pressure at the depth of the top of the block to be P0, and at the bottom of the block to be P1. So (being 4h the height of the block, and A its top & bottom area):
P1 = P0 + ρ_oil*h*g + ρ_water*3h*g
When I work out the forces on the block (the weight of the oil above, the pressure on the bottom of the block) I'd get a balance:
P1*A = W + P0*A
Replacing the values we got the same value of density, 950 kg/m^3.

What is breaking my brain is the fact that I considered the buoyant force of the oil on the block to be upwards, while my friend considered it to be downwards on the block.

I want to know what is the real free-body diagram for the block and is the oil pushing down on the block or pulling it up?

Oil can't pull up on anything.

Like a lot of physical problems, a solution can be obtained using more than one approach. You and your friend have encountered such a problem and obtained the same result.

Remember, the buoyant force on a floating object is produced by the object displacing the fluid in which is floats. This displacement of fluid creates a pressure field which acts over the wetted surface of the object. By Pascal's Law, the pressure acts normal to the wetted surface and the magnitude of the pressure difference is proportional to the depth of the fluid.

If an object is submerged in a fluid but not resting on the bottom of the container, there will be a hydrostatic pressure acting on the upper surface, just like there is a hydrostatic pressure acting on the bottom surface. The net force acting on the block will be:

Fnet = Pbot*Abot - Ptop*Atop

For a wall-sided block, Atop = Abot = A and

Fnet = Pbot*A - Ptop*A = A*(Pbot - Ptop) = A*ΔP

We know from Pascal's Law that ΔP = ρgΔH, so

Fnet = ρgΔH*A = ρgV, where V is the volume of displaced fluid.

Et voila!, as the French say, we have established Archimedes' Principle.

If you want to draw a FBD for this problem, you would have one force to represent the weight of the block and two buoyant forces acting in the direction opposite of the weight: one buoyant force is due to the amount of water displaced, and the other is due to the amount of oil displaced. The two buoyant forces added together would equal the weight of the block.

 

[256bits]

When I work out the forces on the block (the weight of the oil above, the pressure on the bottom of the block) I'd get a balance:
P1*A = W + P0*A

Doesn't that equation represent the FBD of the actual vertical forces acting of the block.
Draw out the block and the vertical forces.

You would have:
P1 of the water acts on the bottom surface upwards.
W of the block due to gravity acts downwards.
P0 of the oil acts on the top surface of the block downwards.

 

[nasu]

What is breaking my brain is the fact that I considered the buoyant force of the oil on the block to be upwards, while my friend considered it to be downwards on the block.

No, he didn't. The pressure exerted by oil on top (times area) is not the buoyant force. The buoyant force comes from a difference in pressure.
If you want the oil's contribution to the buoyant force you need to take (p2-p0) where p2 is the pressure at the interface. Which you implicitly did when you wrote the buoyant force in your treatment.

So there is no contradiction between the two methods. His is about overall buoyant force, yours add the components explicitly.

 

[sophiecentaur]

What is breaking my brain is the fact that I considered the buoyant force of the oil on the block to be upwards, while my friend considered it to be downwards on the block.

The "buoyant force" is the resultant of the two liquids. The effect of the oil is not 'buoyant'.
The oil on the top surface of the cylinder is pushing Down. The water on the bottom surface is pushing Up. In the equilibrium condition, the upward force equals the downward force of the oil and the weight of the cylinder. The magnitudes of pressures on the faces, relative to the liquid interface are ρhg. Signs must be taken into account of course, when writing the equation.

 

[danjordan]

Thanks to all for your messages.
So what I've gathered, to sum up the previous comments, is that both liquids (and I'd guess any number of fluids where a solid is inside) generate a net buoyant force which is due to the difference in pressures. This buoyant force can be analyzed in its components which are given by the amount of fluid displaced by each part of the object in the liquids. So I can say a net buoyant force opposes the object's weight and analyze it's (imaginary, non-physical) components. Kind of like when we treat friction as a force on it's own, but it's physically part of the reaction force of the surface.
On the other hand, and equally valid, I can calculate the net force on the object using the pressure at the bottom and the weight of the oil on top. In fact its mathematical expression is equivalent to the equation using components of the buoyant force, just by rearranging the factors.

I was wrong thinking that the oil was pulling up on the object, because it isn't physically producing a buoyant effect. It's the whole thing, the oil and the water which produce a net force upwards. In fact, without the oil, the water would be under so much pressure and the object would actually sink a little more.
Thanks to all for helping me clear that up :)

 

[abitslow]

I don't understand what you just said. Something about pressure. Things exhibit buoyant forces because of g.r.a.v.i.t.y., fluid flow, and differences in density. The force is indeed the sum of the weights of (as opposed to "amount of") fluids displaced less the weight of the submerged object. You certainly can use the term "oppose" when describing forces acting in opposition, I suggest you may want to be careful with that since force is a vector quantity and only in the most simplistic cases are forces co-linear (directly in line or directly opposed). Pressure is caused by gravitational force, but it is also caused by other sources of compression. Most fluids are almost incompressible (similar to most solids) and small volume reductions create enormous pressures. Picture a blob of water (or an oil and water blob) in space (free fall, microgravity). Add your block. What will happen?
Is it correct to say that the blob is under no pressure?

 

[danjordan]

I don't understand what you just said. Something about pressure. Things exhibit buoyant forces because of g.r.a.v.i.t.y., fluid flow, and differences in density. The force is indeed the sum of the weights of (as opposed to "amount of") fluids displaced less the weight of the submerged object. You certainly can use the term "oppose" when describing forces acting in opposition, I suggest you may want to be careful with that since force is a vector quantity and only in the most simplistic cases are forces co-linear (directly in line or directly opposed). Pressure is caused by gravitational force, but it is also caused by other sources of compression. Most fluids are almost incompressible (similar to most solids) and small volume reductions create enormous pressures.

I agree what you said about buoyant forces, but in this case it's hydrostatics, so fluid flow is something else. Also, no variation in density is being considered, so that part of the comment doesn't help here.
I think I can say "oppose" just fine in this case because shear forces do not come up in hydrostatics, so whatever forces appear will generate a net force co-linear with the weight of the object.
In the part where I said "amount of" I meant it is part of the component, as in it's a factor in the equation.

Picture a blob of water (or an oil and water blob) in space (free fall, microgravity). Add your block. What will happen?
Is it correct to say that the blob is under no pressure?

In such a case, we can watch the videos from astronauts in the space station such as this one
Blobs of water tend to stay unified. They're certainly under pressure due to the air around them. In the vacuum you couldn't have that bubble because there wouldn't be anything to keep it under pressure so it just "evaporates".
From the video you can see that the object inside the bubble doesn't float anywhere, it just stays put.

 

[DaTario]

I guess we can make the two approaches meet harmonically by considering the very small modification (see figure) to be done on the solid.
By creating an artificial surface near the interface oil-water one may observe the formation of a well defined (pedagogically defined) boyance force in the oil and also one in the water.
Nevertheless the force due to the oil (upward) on this artificial surface and due to the water (downward) tend to cancel out as we bring these surfaces closer and closer. In the limit where the two surfaces meet, the diagram on the right recovers the original look of that on the left. This modification may help one to see and to use the boyance force approach in cases where the object doesn´t have plane surfaces on top and bottom (a sphere, for instance).

 

[sophiecentaur]

Archimedes would be the final arbiter here. It would be easy to calculate the 'Weight of Fluid Displaced' and that would have to be the total buoyant force. Any argument about pressures and where the do or don't apply must still deliver the same answer.
You don't need to saw through the middle of the cylinder and work out forces in the join; you could arbitrarily do that exercise at any point along the cylinder. The forces on the base of the cylinder will be due to the sum of the hydrostatic pressure of both the oil and the water. The force on the top of the cylinder will be due to the hydrostatic pressure of (as it happens) just the oil. If the cylinder is in equilibrium, the Weight Force of the cylinder will be equal to the hydrostatic pressure (times the area) at the bottom, less the hydrostatic pressure (times area) on the top. There will be only one solution for the ratio of lengths of the cylinder.
The same thing applies for any floating body but the Air density is too small to affect the calculation (in most cases). Possibly a massive inflated beach ball could float at a depth which would depend on the Air density.

 

[DaTario]

I think I understand your point, but this figure I upload seems to be applicable to a more general class of shapes (not only prism). Once you can see separetedly the two parts of the body, you can proceed to two isolated body analysis and at the end sum up the forces. As the two "interface" surfaces are nearly at the same vertical position, no matter the densities of the fluids, the force effect at them are similar in modulus but with oposite directions, thus cancelling out. It seems to me as having a pedagogical function, don´t you agree?

 

[sophiecentaur]

I think I understand your point, but this figure I upload seems to be applicable to a more general class of shapes (not only prism). Once you can see separetedly the two parts of the body, you can proceed to two isolated body analysis and at the end sum up the forces. As the two "interface" surfaces are nearly at the same vertical position, no matter the densities of the fluids, the force effect at them are similar in modulus but with oposite directions, thus cancelling out. It seems to me as having a pedagogical function, don´t you agree?

There's no limit to how far you can take this. A prism is the easiest but it's a matter of linking the pressures, directions and forces to the simple idea of displacement. It would depend on the level at which you are teaching as to what you tell 'em.
Splitting an object up into suitable parts can be a good idea.

 

[DaTario]

I was trying to provide a proof to Arquimedes principle, but the obstacle was the diversity of shapes.

 

[sophiecentaur]

I was trying to provide a proof to Arquimedes principle, but the obstacle was the diversity of shapes.

Yes. I see that. Perhaps the best approach is to do it with the simplest example and then with a 'stepped' (ziggurat) shape. To be rigorous would call for Calculus, I would think.
But the order of teaching a topic is always questionable.

 

[DaTario]

But is there a demonstration for this principle (even using calculus)?
Perhaps the word "principle" is already the answer to my question, for otherwise it would be called theorem of Aquimedes...

 

[sophiecentaur]

But is there a demonstration for this principle (even using calculus)?
Perhaps the word "principle" is already the answer to my question, for otherwise it would be called theorem of Aquimedes...

It's easy enough to integrate the components of elemental forces over the area of 'any' solid.
I don't expect that Archimedes was thinking that rigorously, though (a few centuries short of a calculus system) so 'principle' is probably the word for it.

 

[haruspex]

I don't expect that Archimedes was thinking that rigorously,

I have always assumed Archimedes reasoned that the buoyant force can only depend on the 3D envelope of the solid and, possibly, its depth. If that envelope were occupied by more of the fluid instead, the system would be in equilibrium. Therefore the upthrust equals the weight of that occupying fluid.

There is a requirement for applying the principle that is not always appreciated. The fluid must be able to reach all parts of the surface of the object. E.g., consider a rubber suction cup.

Wrt use of calculus, bear in mind that Archimedes effectively discovered integral calculus in his theorem regarding the surface area of a sphere, so I would not rule out his having used such an approach for buoyancy.

 

[sophiecentaur]

The fluid must be able to reach all parts of the surface of the object.

Yep. Definitely.

 

[DaTario]

But it seems that in the case where the fluid is not able to reach all the parts of the surface of an object (like for instance the nautilus sea shell in the figure - perhaps not a perfect example...) we may still define an effective volume which is suitable to the application of Arquimedes Principle. And this effective volume is not an artificial quantity, it is in fact the volume whose border is a closed water surface.

 

[haruspex]

But it seems that in the case where the fluid is not able to reach all the parts of the surface of an object (like for instance the nautilus sea shell in the figure - perhaps not a perfect example...) we may still define an effective volume which is suitable to the application of Arquimedes Principle

Not always. Internal surfaces are not relevant.
Consider an object resting at the bottom of the container and making such close contact with the container that the fluid cannot get between the two. Now the fluid is unable to exert an upward force on the base of the object. This is what happens with a suction cup.

 

[sophiecentaur]

Not always. Internal surfaces are not relevant.
Consider an object resting at the bottom of the container and making such close contact with the container that the fluid cannot get between the two. Now the fluid is unable to exert an upward force on the base of the object. This is what happens with a suction cup.

There is always a temptation to over complicate things and this thread demonstrates it well. The suction cup should be enough to lay this particular ghost perfectly.

 

[DaTario]

It is very interesting in deed, but in the case that the suction cup is sucking a vertical plane surface, the boyance force seems to be regularly defined although the water is not able to reach all the surfaces of the cup.