SUMMARY
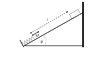
The discussion focuses on calculating the spring constant (K) for a block sliding down an incline and compressing a spring. The block, with a mass of 2 kg, compresses the spring by 0.03 m after sliding down a ramp inclined at 30 degrees. The energy conservation equation used is mgh = 0.5kx², where the gravitational potential energy is converted into spring potential energy. The key conclusion is that the maximum compression of the spring occurs when the block momentarily comes to rest, allowing for the calculation of K using the derived equation mg(L*sin θ) = 0.5k(Δx²).
PREREQUISITES
- Understanding of energy conservation principles in physics
- Familiarity with spring mechanics and Hooke's Law
- Knowledge of trigonometric functions, specifically sine
- Ability to manipulate algebraic equations for solving variables
NEXT STEPS
- Calculate the spring constant K using the derived equation from the discussion
- Explore energy conservation in different mechanical systems
- Study the effects of varying angles on the potential energy of inclined planes
- Investigate real-world applications of springs in mechanical systems
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and energy conservation, as well as educators looking for practical examples of spring dynamics and inclined planes.