- #1
- 10,302
- 1,472
Suppose we have a neutral uncharged square current loop, carrying a constant current I. If we boost it in the x direction, [itex] x' = \gamma \left( x + \beta t \right) [/itex], so that x' increases as t increases (hence the plus sign), what happens to the current?
I get that the current density in the y direction should be unchanged by the boost, but the cross sectional area decreases, so the total current gets divided by gamma. The current density in the x direction increases by gamma, and the area is unchanged, so the total current increases by gamma. In addition, the loop is not neutral everywhere, though the total net charge remains zero. This gives the following picture (the x-axis is from left to right, y runs up the page and + and - represent the charge).
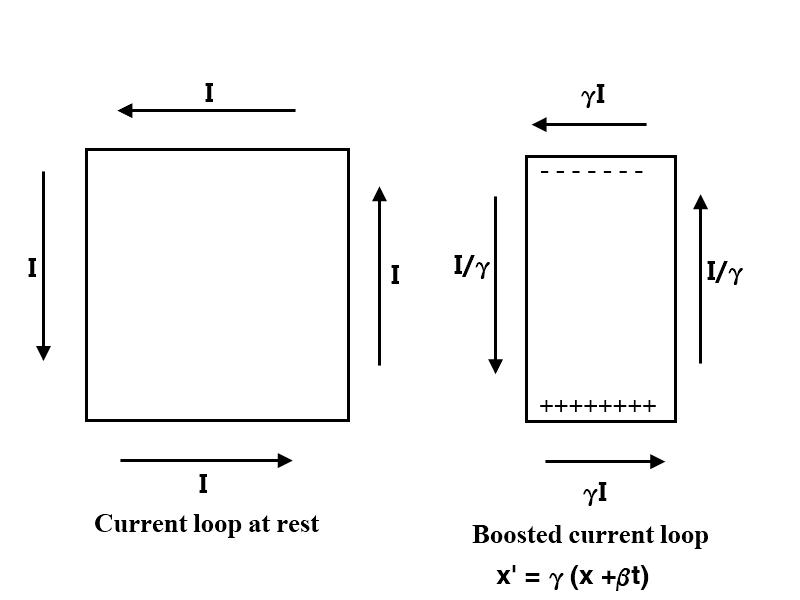
This result is not very intuitive, but I don't see any error in it. I wouldn't mind a second opinion, though the problem seems simple enough. The + and - signs show the charge distribution in the boosted frame.
I was particularly worried about the continuity equation, but if we micro-model the current density in the lower left hand corner in the rest frame as
[tex]J_x = \frac{kX}{L} \hspace{30 mm} J_y = k \frac{y-L}{L} \hspace{30 mm} 0 < x,y < L [/tex]
it seems to satisfy the continuity equations [itex]\nabla_a J^a = 0[/itex] in the rest frame and in the boosted frame.
So it appears to me that Kirchoff's current law takes an apparent hit.
I get that the current density in the y direction should be unchanged by the boost, but the cross sectional area decreases, so the total current gets divided by gamma. The current density in the x direction increases by gamma, and the area is unchanged, so the total current increases by gamma. In addition, the loop is not neutral everywhere, though the total net charge remains zero. This gives the following picture (the x-axis is from left to right, y runs up the page and + and - represent the charge).
This result is not very intuitive, but I don't see any error in it. I wouldn't mind a second opinion, though the problem seems simple enough. The + and - signs show the charge distribution in the boosted frame.
I was particularly worried about the continuity equation, but if we micro-model the current density in the lower left hand corner in the rest frame as
[tex]J_x = \frac{kX}{L} \hspace{30 mm} J_y = k \frac{y-L}{L} \hspace{30 mm} 0 < x,y < L [/tex]
it seems to satisfy the continuity equations [itex]\nabla_a J^a = 0[/itex] in the rest frame and in the boosted frame.
So it appears to me that Kirchoff's current law takes an apparent hit.
Attachments
Last edited:
