Jarek 31
- 157
- 31
- TL;DR
- QM is seen as equivalent with Feynman path ensemble, Ising model as Boltzmann - can we use their mathematics similarity to get some intuitions?
Quantum mechanics is often said to be equivalent with Feynman path ensemble, which "after Wick rotation" becomes Boltzmann path ensemble, also called euclidean path integrals (popular for numerical calculations), or random walk/diffusion MERW (maximal entropy random walk).
But Boltzmann path ensemble is also believed to have classical solid state realization - 1D Ising model: Boltzmann distribution among spatial sequences e.g. of spins.
This mathematical similarity suggests question if we can transfer some concepts between them, like Born rule, Bell violation, quantum computers?
Let me start with Born rule, mathematical similarity allows to see something like it in Ising model e.g. if asking: what is the probability distribution of values in given position of Ising sequence?
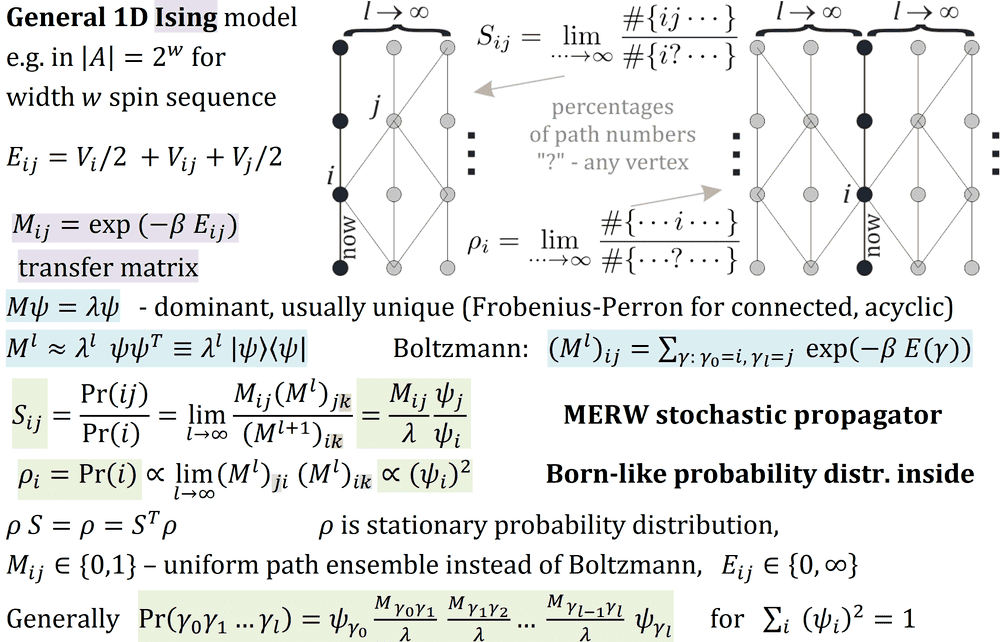
Let me sketch derivation for general case: in each position there is a value from ##A## set, e.g. up or down spin, or something more complex like ##2^w## possible spin configurations for sequence of width ##w## spins (2D ##w\times \infty## Ising model as 1D of width ##w##).
We need to define ##E_{ij}: i,j\in A## matrix of energy for neighbors, Ising model is Boltzmann distribution using energy of path ##\gamma## as ##E(\gamma)=\sum_t E_{\gamma_t , \gamma_{t+1}}##.
We define transfer matrix ##M_{ij} =\exp(-\beta E_{ij})##, its power ##M^l## can be imagined as containing Boltzmann ensemble of length ##l## paths.
Usually ##M## matrix has dominant eigenvalue ##M\psi = \lambda \psi## (Frobenius-Perron theorem), allowing to use asymptotic behavior ##M^l \approx \lambda^l \psi \psi^T ##.
Now to find probability distribution in a given position, we can take ensemble of paths ##l## steps toward left and toward right, and perform limit
##Pr(i) \propto \lim_{l\to\infty} (M^l)_{ji} (M^l)_{ik} \propto (\psi_i)^2##
Can it be seen as Born rule?
What is the differences from quantum Born rule?
Diagram:
But Boltzmann path ensemble is also believed to have classical solid state realization - 1D Ising model: Boltzmann distribution among spatial sequences e.g. of spins.
This mathematical similarity suggests question if we can transfer some concepts between them, like Born rule, Bell violation, quantum computers?
Let me start with Born rule, mathematical similarity allows to see something like it in Ising model e.g. if asking: what is the probability distribution of values in given position of Ising sequence?
Let me sketch derivation for general case: in each position there is a value from ##A## set, e.g. up or down spin, or something more complex like ##2^w## possible spin configurations for sequence of width ##w## spins (2D ##w\times \infty## Ising model as 1D of width ##w##).
We need to define ##E_{ij}: i,j\in A## matrix of energy for neighbors, Ising model is Boltzmann distribution using energy of path ##\gamma## as ##E(\gamma)=\sum_t E_{\gamma_t , \gamma_{t+1}}##.
We define transfer matrix ##M_{ij} =\exp(-\beta E_{ij})##, its power ##M^l## can be imagined as containing Boltzmann ensemble of length ##l## paths.
Usually ##M## matrix has dominant eigenvalue ##M\psi = \lambda \psi## (Frobenius-Perron theorem), allowing to use asymptotic behavior ##M^l \approx \lambda^l \psi \psi^T ##.
Now to find probability distribution in a given position, we can take ensemble of paths ##l## steps toward left and toward right, and perform limit
##Pr(i) \propto \lim_{l\to\infty} (M^l)_{ji} (M^l)_{ik} \propto (\psi_i)^2##
Can it be seen as Born rule?
What is the differences from quantum Born rule?
Diagram: