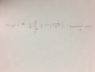Boundary Potential Problem- parallel alternating potential

[ebru]

Homework Statement

Hello,
I have a question about the potential. I think the potential shoul be something like below. In that way periodic behavior work perfectly. But I don't know how to add the x variable to the equation.

Relevant Equations

So how can I find potential?

 

[Antarres]

Well this amounts to solving a Laplace equation for potential, right?
$$\Delta \phi = -\frac{\rho}{\epsilon} = 0$$
I would solve this 2D Laplace equation for a rectangle defined by $0<x<a$ and $0<y<b$. Then once you have the potential inside that rectangle, you would periodically extend it over $y$. I assume you're familiar with this equation since you're asking this kind of a question, if you're not, I can give you some introduction to it in the next post.