norcal36
- 8
- 0
- Homework Statement
- You have two scales with a weight suspended from them on a string. Scale one has a tension of T1 and scale two has its mass submerged in water with tension T2. If you have T2<T1, find the density of the weight in terms of only density of the water, T1 and T2.
- Relevant Equations
- Density = mass/volume
Volume = mass/density
mass = density*volume
Buoyancy = Density of liquid*Volume Displaced*gravity
Hi new to the physics world and the symbiology is hard to understand completely. Attached is the work I've done to a final solution but I can't seem to get the answer in terms of only density of water and T1 and T2. Thank you for any assistance.
[ Mentor Note -- Word file replaced with a screenshot. Please use PDF or JPEG format for posting files. ]
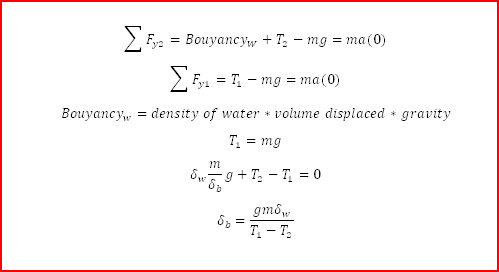
[ Mentor Note -- Word file replaced with a screenshot. Please use PDF or JPEG format for posting files. ]
Last edited by a moderator:
 ##\qquad## !
##\qquad## !