- #1
DoobleD
- 259
- 20
Is it possible to build the full wave function for a simple problem in QM, such as an infinite well, without any experimental data ?
I'm learning about QM, and I saw how to compute energy states (the wave function for each allowed energy level) in some usual QM basic problems. But then, I was always given the probabilities for energy state, so that I could build the "full" wave function (sum of all possible energy state, each multiplied by its probability); OR, I was given a full wave function so that I could compute the probability for each state by taking the inner product of the full wave function with each energy state.
Is it possible to build a full wave function, which is the sum of all possible energy state each with its probability coefficient, from scratch ?
In the case of the infinite well, or an other simple problem, what would be the procedure once you computed the possible energy state ?
Here is the question reformulated below with equations which I think is much clearer :
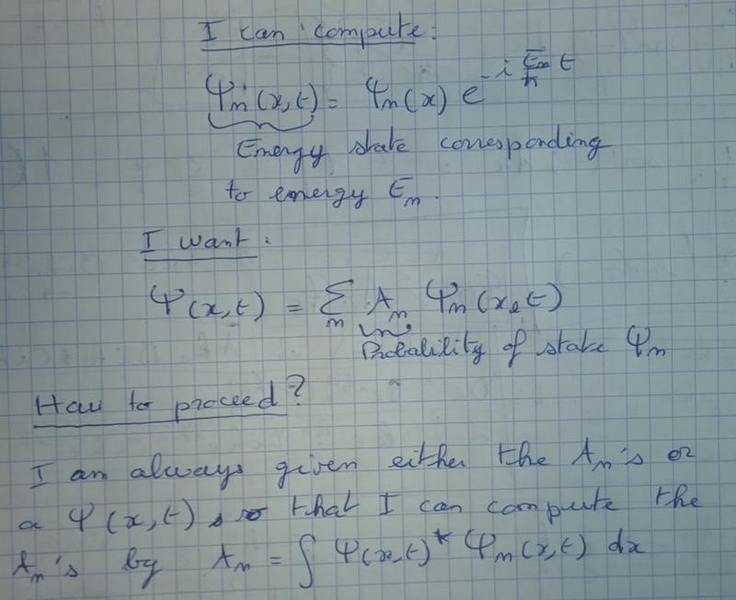
I'm learning about QM, and I saw how to compute energy states (the wave function for each allowed energy level) in some usual QM basic problems. But then, I was always given the probabilities for energy state, so that I could build the "full" wave function (sum of all possible energy state, each multiplied by its probability); OR, I was given a full wave function so that I could compute the probability for each state by taking the inner product of the full wave function with each energy state.
Is it possible to build a full wave function, which is the sum of all possible energy state each with its probability coefficient, from scratch ?
In the case of the infinite well, or an other simple problem, what would be the procedure once you computed the possible energy state ?
Here is the question reformulated below with equations which I think is much clearer :
Last edited: