By choosing a suitable value of x, sum the series

[bubokribuck]

The question:

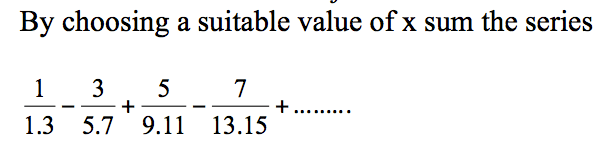Here's my thought so far:

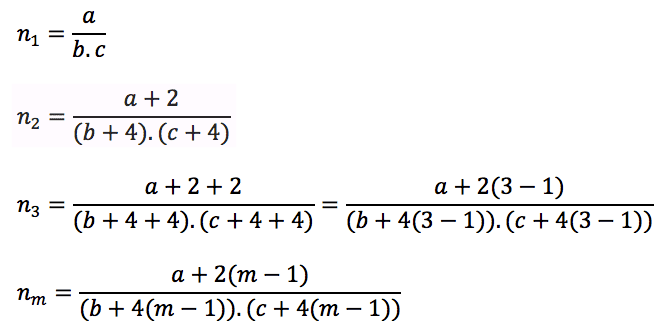This is pretty much what I have come up with. However, I don't know how to find a general solution for the sum of the series. Can someone help please. (the decimal part is where I'm stuck the most)

 

[SammyS]

The question:

...

$\displaystyle\frac{1}{1\cdot3}-\frac{3}{5\cdot7}+\frac{5}{9\cdot11}-\frac{7}{13\cdot15}+\dots$

What do we see?

The signs of the terms alternate.

Each successive numerator is the next odd natural number. If n is the index and starts at 0, then each numerator is (2n-1).

How are the two factors in each denominator related to each numerator ? (Consider what 2 times the numerator is for each.)

 

[Joffan]

My guess is that those are not decimal points - they are multiplication dots.

Presumably you have noticed the alternating signs on the terms.

There is a simple relationship between the numerator and the two terms in the denominator in each term which will probably help.

 

[bubokribuck]

$\displaystyle\frac{1}{1\cdot3}-\frac{3}{5\cdot7}+\frac{5}{9\cdot11}-\frac{7}{13\cdot15}+\dots$

What do we see?

The signs of the terms alternate.

Each successive numerator is the next odd natural number. If n is the index and starts at 0, then each numerator is (2n-1).

How are the two factors in each denominator related to each numerator ? (Consider what 2 times the numerator is for each.)

Um... to be honest, I can't see how each denominator relates to each numerator, doesn't seem like there's a sequence.

 

[bubokribuck]

My guess is that those are not decimal points - they are multiplication dots.

Presumably you have noticed the alternating signs on the terms.

There is a simple relationship between the numerator and the two terms in the denominator in each term which will probably help.

Yes I have noticed the alternating signs, but couldn't find any relationship between the numerator and the denominator though :(

 

[Joffan]

Well, calculate out the first ten terms, then come back and post them all.

$+\frac{1}{1\times3}$

$-\frac{3}{5\times7}$

$+\frac{5}{9\times11}$

$-\frac{7}{13\times15}$

$\ldots$

 

[Joffan]

You might also put in the known values for a, b and c (1,1,3) in your formula for $n_{m}$ and simplify.

 

[SammyS]

Um... to be honest, I can't see how each denominator relates to each numerator, doesn't seem like there's a sequence.

Compare the factors in each denominator to 2 times the numerator !

 

[spamiam]

Each successive numerator is the next odd natural number. If n is the index and starts at 0, then each numerator is (2n-1).

Just a small typo--I'm guess you meant the numerator is 2n+1.

bubokribuck: What is the first part of this problem (that you've cut off from the image you posted)? The statement of the problem ("By choosing a suitable value of x...") indicates that in previous parts of this problem you've found a series representation for some function, which you are supposed to use to solve this part.

 

[bubokribuck]

Just a small typo--I'm guess you meant the numerator is 2n+1.

bubokribuck: What is the first part of this problem (that you've cut off from the image you posted)? The statement of the problem ("By choosing a suitable value of x...") indicates that in previous parts of this problem you've found a series representation for some function, which you are supposed to use to solve this part.

Hi spamiam, here's the full question, but I don't like it has anything to do with the previous parts though.

 

[bubokribuck]

Well, calculate out the first ten terms, then come back and post them all.

$+\frac{1}{1\times3}$

$-\frac{3}{5\times7}$

$+\frac{5}{9\times11}$

$-\frac{7}{13\times15}$

$\ldots$

Hi Joffan, here it is.

 

[bubokribuck]

Just a small typo--I'm guess you meant the numerator is 2n+1.

If the first term is n=1, then the numerator of the first term would be 2n-1 right? (as 2(1)-1=1)

 

[bubokribuck]

Compare the factors in each denominator to 2 times the numerator !

Ah, I think I am getting it now!

Let N denotes the numerator, and D denotes the denominator, then D=(2N-1)(2N+1). Is this right? So for the nth term, it would be something like (-1)ⁿ⁺¹$\frac{2n-1}{(4n-3)(4n-1)}$

 

[spamiam]

Hi spamiam, here's the full question, but I don't like it has anything to do with the previous parts though.

It definitely has to do with the previous part! What could you be choosing x for if not to plug into the Fourier series you found in an earlier part? So what did you get for the first 2 parts? In particular, what did you get for the Fourier series of the function?

You formula for the general term of the series looks correct.

 

[SammyS]

Just a small typo--I'm guess you meant the numerator is 2n+1.

bubokribuck: What is the first part of this problem (that you've cut off from the image you posted)? The statement of the problem ("By choosing a suitable value of x...") indicates that in previous parts of this problem you've found a series representation for some function, which you are supposed to use to solve this part.

If the index, n, starts at zero, (like I said), then, yes, that should be (2n+1).

 

[bubokribuck]

It definitely has to do with the previous part! What could you be choosing x for if not to plug into the Fourier series you found in an earlier part? So what did you get for the first 2 parts? In particular, what did you get for the Fourier series of the function?

You formula for the general term of the series looks correct.

Hi spamiam, here's what I've got for the Fourier series:

And here's the sigma equation I've come up with for the last part of the question.

 

[spamiam]

Hi spamiam, here's what I've got for the Fourier series:

And here's the sigma equation I've come up with for the last part of the question.

Hm, that's not what I get for the Fourier series. Could you show your calculations? Also, your series has a couple of oddities. For one thing, when n=1, you have terms of the form 1/0. Hopefully this doesn't pose a problem since these terms should cancel out. Which brings me to the second observation--you can simplify your sum since terms cancel out when n is odd.

 

[bubokribuck]

Hm, that's not what I get for the Fourier series. Could you show your calculations? Also, your series has a couple of oddities. For one thing, when n=1, you have terms of the form 1/0. Hopefully this doesn't pose a problem since these terms should cancel out. Which brings me to the second observation--you can simplify your sum since terms cancel out when n is odd.

Hi, the calculations are quite long, so I've attached a document. :)

 

[spamiam]

Hi, the calculations are quite long, so I've attached a document. :)

Hey bubokribuck,

I (and I'm guessing this is the case with most other members from the 0 views your attachment has gotten) am wary of downloading zip files as a general rule. Could you upload it in another format like .doc, .pdf, or .jpg?

 

[bubokribuck]

Hey bubokribuck,

I (and I'm guessing this is the case with most other members from the 0 views your attachment has gotten) am wary of downloading zip files as a general rule. Could you upload it in another format like .doc, .pdf, or .jpg?

Hi, the doc exceeds the upload size limit, therefore I can only upload png. Thanks :)

 

[spamiam]

Hi, the doc exceeds the upload size limit, therefore I can only upload png. Thanks :)

Much better. I think your work is correct. I solved the integral differently, using to applications of integration by parts. As I said before, you really need to simplify your answer. I think you have a correct expression, but you need to combine your terms and put them over a common denominator.

The earlier parts of the problem are supposed to help later on! They can really save you a lot of work. For instance, I knew by inspection that all the $a_n$ were 0 just by observing that f is an odd function. Similarly, you can simplify the calculation of the $b_n$ by noting that the integrand is even.

So try simplifying your answer. Look for cancellation in terms of the form $(-1)^k + 1$, too. I think this will make the choice for x a lot easier.

 

[bubokribuck]

Much better. I think your work is correct. I solved the integral differently, using to applications of integration by parts. As I said before, you really need to simplify your answer. I think you have a correct expression, but you need to combine your terms and put them over a common denominator.

The earlier parts of the problem are supposed to help later on! They can really save you a lot of work. For instance, I knew by inspection that all the $a_n$ were 0 just by observing that f is an odd function. Similarly, you can simplify the calculation of the $b_n$ by noting that the integrand is even.

So try simplifying your answer. Look for cancellation in terms of the form $(-1)^k + 1$, too. I think this will make the choice for x a lot easier.

Hi spamiam, I don't seem to be able to cancel out the terms, is there something I've done wrong?

 

[spamiam]

Hi spamiam, I don't seem to be able to cancel out the terms, is there something I've done wrong?

Looks good! The only tiny mistake I see is that you've forgotten the factor of $1/\pi$ during the course of your calculation. One other thing you might want to do is pull out a factor of -1 from $(-1)^{n+1} - 1$.

Now write out the series for f again using your simplified version of the b_n. This is where the cancellation comes into play. What is the value of b_n if n is odd? How does this eliminate terms from the sum?

 

[bubokribuck]

Looks good! The only tiny mistake I see is that you've forgotten the factor of $1/\pi$ during the course of your calculation. One other thing you might want to do is pull out a factor of -1 from $(-1)^{n+1} - 1$.

Hum... I'm not quite sure how to do that, the furthest I can go is:

$(-1)^{n+1} - 1$

= $(-1)^n(-1)^1 - 1$

= $-(-1)^n - 1$

But the problem is when n=1, the denominator is still equal to zero (which is obviously wrong).

 

[spamiam]

Hum... I'm not quite sure how to do that, the furthest I can go is:

$(-1)^{n+1} - 1$

= $(-1)^n(-1)^1 - 1$

= $-(-1)^n - 1$

It doesn't really matter, but it's just $(-1)^{n+1} - 1 = (-1)(-1)^n + (-1)1 = -((-1)^n +1)$. You can stick that negative in the denominator if you like.

But the problem is when n=1, the denominator is still equal to zero (which is obviously wrong).

Yes, this is somewhat strange, but I think it's okay, because if n=1, then the numerator is zero, too.

So, as I said before, write out the Fourier series again and look for cancellation when n is odd or even.