- #1
Ryaners
- 50
- 2
[Please excuse the screengrabs of the fomulae - I'll get around to learning TeX someday!]
1. Homework Statement
Find the sum of this series (answer included - not the one I'm getting)
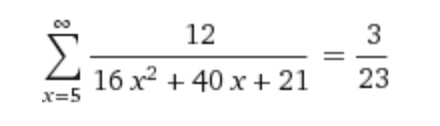
So I'm trying to sum this series as a telescoping sum. I decomposed the fraction and the partial sum collapses down to this:
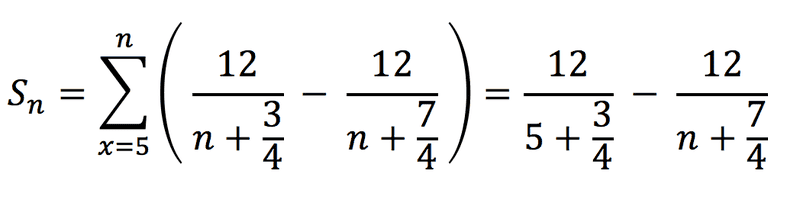
Then when I take the limit, the second term vanishes, leaving just the first term as the final value, i.e.:
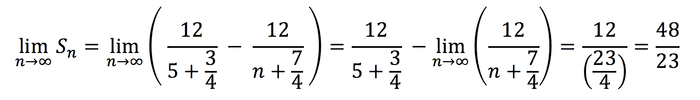
Needless to say 48/23 ≠ 3/23
I can't see what I'm doing wrong - I've triple-checked everything & must be misunderstanding something fundamentally speaking. The partial fraction decomposition is (to the best of my / Wolfram A's knowledge) correct. Can anyone point out my mistake(s)?
1. Homework Statement
Find the sum of this series (answer included - not the one I'm getting)
The Attempt at a Solution
So I'm trying to sum this series as a telescoping sum. I decomposed the fraction and the partial sum collapses down to this:
Then when I take the limit, the second term vanishes, leaving just the first term as the final value, i.e.:
Needless to say 48/23 ≠ 3/23

I can't see what I'm doing wrong - I've triple-checked everything & must be misunderstanding something fundamentally speaking. The partial fraction decomposition is (to the best of my / Wolfram A's knowledge) correct. Can anyone point out my mistake(s)?
