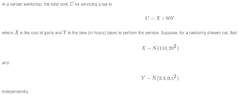Calc Expected Value & Variance of Multivar. Func.

[TheFallen018]

Hey, I've got this problem that I've been trying to crack for a while. I can't find any info for multi-variable expected values in my textbook, and I couldn't find a lot of stuff that made sense to me online. Here's the problem.

View attachment 8906
Find $E(C)$
Find $Var(C)$

I tried to get the limits from the normal distributions that were given. If I was doing it right, I had
$90\leq X \leq 130 $
$1.9\leq Y \leq 2.9$
for X and Y.

I think my main problem is that I'm not sure how to get $f(x)$ and $f(y)$ so that I can use the property
$E(aX+bY) = aE(X)+bE(Y)$
and
$E(x) = \int_{n}^{m}x*f(x)dx$
where $n \leq f(x) \leq m$.

I think I might be able to figure it out once I can work out what the functions should be, but I'm a little stuck here. Any help would be awesome. Thanks.

 

[HOI]

You are told that X is normally distributed with mean 110 and standard deviation 20 (I am assuming that the second number, "$20^2$" is the variance that is the square of the standard deviation.) Whoever gave you this problem clearly expects you to know what the "normal distribution" is! The "f(x)" you want is $\frac{1}{\sqrt{2(\pi)(20^2)}}e^{-\frac{(x- 110)^2}{2(20^2)}} = \frac{1}{20\sqrt{2\pi}}e^{\frac{(x- 110)^2}{800}}$ and similarly for g(y). (You have "f(x)" and "f(y)" but they are not the same function!)

Look at https://en.wikipedia.org/wiki/Normal_distribution