Discussion Overview
The discussion revolves around calculating the radius of curvature and the center of a circle with respect to a curve, as well as the concept of improper integrals. Participants explore the mathematical formulations and reasoning behind these concepts, including the use of derivatives and limits.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant inquires about the calculation of the radius of curvature and the center of a circle related to a curve, expressing uncertainty about improper integrals.
- Another participant provides a formula for the radius of curvature involving first and second derivatives.
- A different participant illustrates an example of an improper integral and its evaluation using limits.
- Concerns are raised about the necessity of the second derivative in the radius of curvature formula, with one participant suggesting that the first derivative might suffice.
- Another participant questions the reasoning behind raising the square root term to the power of three in the curvature formula.
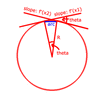
- A participant presents their own method for finding the radius of curvature, involving tangent slopes and arc length calculations, and seeks feedback on potential mistakes.
- There is a discussion about the formula for arc length, with one participant challenging the steps taken by another and suggesting a standard formula for differential arc length.
- Clarifications are made regarding the use of the distance formula between two points on a curve and the implications of taking limits as the distance approaches zero.
- One participant expresses gratitude for the insights gained during the discussion, indicating a better understanding of the radius of curvature concept.
Areas of Agreement / Disagreement
Participants express differing views on the necessity of the second derivative for calculating the radius of curvature and the correct formulation of arc length. The discussion includes multiple competing approaches and remains unresolved on certain technical points.
Contextual Notes
Some participants' calculations and assumptions about limits and derivatives are not fully aligned, leading to confusion about the correct application of formulas. The discussion reflects varying levels of understanding regarding the mathematical principles involved.