Calculate a radius of a circle on a screen

[Lotto]

Homework Statement

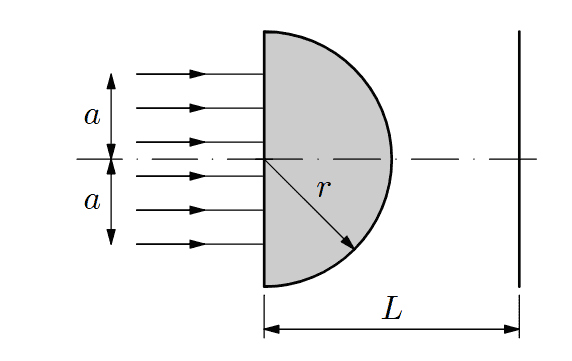
On a flat surface of a glass hemisphere with a radius of $r = 4.0 \,\mathrm {cm}$ with a refractive index $n= 1.50$, a circular bundle of parallel beams with a diameter of $2a = 6.0 \,\mathrm{cm}$ falls parallel to the optical axis. What will be the radius $R$ of the illuminated circle on a screen, which is positioned perpendicular to the optical axis at a distance of $L = 8.0\,\mathrm{ cm}$ from the plane area of the hemisphere? A picture below.

Relevant Equations

$f=\frac{n_1 n_2 R_1 R_2}{(n_2-n_1)[(n_2-n_1)d+n_2(R_2-R_1)]}$

The picture is here. The radius should be $R=2.94\,\mathrm {cm}$.

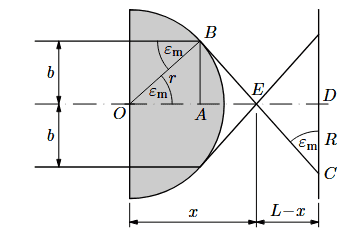
In the original solution, it is solved by using a critical angle ϵm. The b is the maximum distance at which a beam can refract. I understand this solution and an image of it is here:

But I wanted to calculate it by knowing that the hemosphere is a thick lens. I calculated its focal lenght to be $f=8.0\,\mathrm {cm}$ and that its one principal axis touches the top of the lens. So the focus F′ should be $4\,\mathrm{ cm}$ behind the screen.

The light beams are parallel to the optical axis, so they should refract into the focus F′, but according to the picture, that is not true. I tried to calculate the radius $R$ by using that focal lenght and my value is wrong.

I understand that not all bems refract after passing through the lens, but why cannot I use the focal lenght and solve the problem by using thick lens knowledge? Or where are my thoughts wrong?

 

[kuruman]

The lens maker's formula is an approximation also known as the thin lens approximation that applies to thin lenses. If you carefully trace rays through the hemisphere, you will see that not all rays converge to the same focal point.

 

[Lotto]

The lens maker's formula is an approximation also known as the thin lens approximation that applies to thin lenses. If you carefully trace rays through the hemisphere, you will see that not all rays converge to the same focal point.

Yes, I understand that the formula for the focal lenght is only a paraxial approximation, but it is still weird that the focus error is so big. Because I suppose that accroding to the second picture, the focus is at point $E$.

And the formula above is for a thick lens of a thickness $d$.

 

[kuruman]

And the formula above is for a thick lens of a thickness $d$.

Here we have a hemisphere of thickness $R$. Furthermore, the formula assumes that rays are refracted past point $b$ in the second diagram which means internal reflection (which you know is there) is disregarded.

Do yourself a favor and a relatively simple calculation.
Let $y=$ the distance from the optical axis to where the ray enters the flat face of the hemisphere.
Let $x=$ the distance from the center of the flat face to where the exiting refracted ray crosses the optical axis on the other side.

Calculate $x$. If it is independent of $y$, then a focal length exists. If it is not, then a focal length does not exist and the thick lens equation that you used does not apply to the hemisphere.