Calculate (and argue) the critical points of an exponential function

[mcastillo356]

Homework Statement

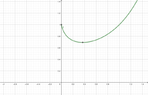
Calculate the critical point of $y=x^x$

Relevant Equations

Chain Rule, Product Rule

Hi everybody

We can't differentiate $x^x$ neither like a power function nor an exponential function. But $x^x=e^{x\mbox{ln}x}$. So

$\dfrac{d}{dx}x^x=\dfrac{d}{dx}e^{x\mbox{ln}x}=x^x(\mbox{ln}x+1)$

And here comes the doubt: prove the domain of $x^x$ is $(0, +\infty)$

Why is only positive?; why it will never be 0?

So $(\mbox{ln}x+1)=0\Rightarrow{x=1/e}$

It's a solved exercise at Calculus, by R.A.A. It's the only question not solved (the domain, I mean).

 

[PeroK]

You can define $0^0$ if you want, but fractional powers of negative numbers are undefined, or require complex numbers. E.g. $-0.5^{-0.5}$ is not a real number.

 

[mcastillo356]

Can $0^0=1$? The book says: $x^x$ is never 0. This is the graph:



$0^x=0$ on one hand; $x^0=1$. This is all I can provide.

 

[fresh_42]

$0^0$ is given a value per definition. If you want continuity of $x \longrightarrow x^0$ at $x=0$ then you have to set $0^0=1,$ and if you want continuity of $x\longrightarrow 0^x$ at $x=0$ then you have to set $0^0=0.$

My personal opinion is, that only $0^0=1$ is a valid definition because exponentiation is an abbreviation for multiplication and all multiplications over an empty set of indexes equals the neutral element of multiplication, which is $1.$
$$
\sum_{i\in \{\}} a_i = 0 \quad ;\quad \prod_{i\in \{\}} a_i = 1
$$

 

[mcastillo356]

The next step would be to prove $\displaystyle\lim_{x \to{0+}}{x^x}=f(0)=1$? I am just wondering.

 

[fresh_42]

The next step would be to prove $\displaystyle\lim_{x \to{0+}}{x^x}=f(0)=1$? I am just wondering.

Yes. E.g. we get for $x>0$
$$
\lim_{n \to \infty}\left(\dfrac{1}{n}\right)^{1/n}= \lim_{n \to \infty}\left(1-\dfrac{\log n}{n}+O(n^{-2})\right)=1.
$$
But if you decouple base and exponent, say $f(x,y)=x^y,$ then all depends on which path you approach $(0,0).$ That is where the question: "Why isn't $0^0=0$ ?" comes from. $x\longmapsto x^x$ and $(x,y)\longmapsto x^y$ are different functions with different properties. And even $f(x,y)$ depends on its domain: real positive numbers, all real numbers and complex values, complex numbers and complex values. These are questions that should be answered before we discuss $0^0.$ The answer depends on them.

 

[mcastillo356]

$\displaystyle\lim_{x \to{0^+}}{e^{x\ln(x)}}=e^{\lim_{x \to{0^+}}{x\ln(x)}}=e^{\lim_{x \to{0^+}}{\frac{\ln(x)}{1/x}}}$, and, by L'Hopital, $\displaystyle e^{\lim_{x \to{0^+}}{-x}}=1$.

Is this equal to $f(0)$? Don't know. $x^x=e^{x\ln(x)}$. Does this alow me to say "no", because $\ln 0$ is nonsense?.

 

[fresh_42]

$\displaystyle\lim_{x \to{0^+}}{e^{x\ln(x)}}=e^{\lim_{x \to{0^+}}{x\ln(x)}}=e^{\lim_{x \to{0^+}}{\frac{\ln(x)}{1/x}}}$, and, by L'Hopital, $\displaystyle e^{\lim_{x \to{0^+}}{-x}}=1$.

This is correct.

Is this equal to $f(0)$? Don't know. $x^x=e^{x\ln(x)}$. Does this alow me to say "no", because $\ln 0$ is nonsense?.

What do you mean? "No" as an answer to what? And where do you have $\log 0$ if you use de L'Hôpital?
You could as well use a Taylor expansion of $\log$ and observe that $y=x$ goes faster to zero than $y=\log x$ does so that the product goes to zero. Taylor will give you a quantitative measure for "faster than".

 

[mcastillo356]

Another try

In the exercise I'm given a function $f(x)=x^x$. We have $x^x:=e^{x\ln x}$, which is well defined for $x>0$, so the domain is $(0,\infty)$.

Now, we can define another function $[0,\infty)\rightarrow{\mathbb R}$ such that

$$g(x):=\begin{cases}{f(x)}&\text{if}& x\in{(0,\infty)}\\1 & \text{if}& x=0\end{cases}$$

Where we assume $0^0:=1$

 

[fresh_42]

You can define $g(x)$ whichever you want. The question is: which properties do you require? If you do it like this, then we get a continuous extension of $f(x)$.

 

[mcastillo356]

Hi, fresh_42

The question is: which properties do you require?

No idea. I'm afraid I let myself struggle with maths with lots of naivety. Sooo...PF is a great, great, help, and a place where I feel at home, an island of give-and-take knowledge.

But I think I generate expectations I'm not able to tackle...

Conclusion: Thanks for helping me one more time. Much love. Forgive me if this post is improper. I felt I had to contextualize the thread.