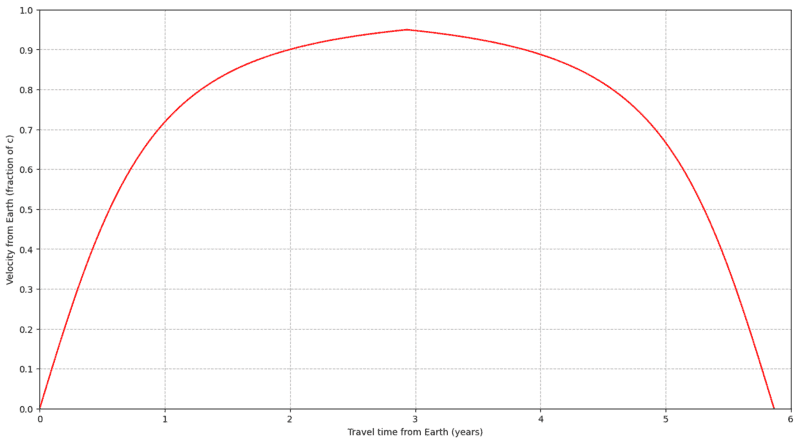
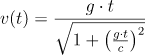##\DeclareMathOperator{\sinh}{sinh}\DeclareMathOperator{\sech}{sech}##I thought I would work this out.
Let's call the distance from Earth to Proxima ##L##, and say the rocket accelerates at constant proper acceleration ##\alpha##. Given a set of inertial coordinates ##T,X## we can define a set of Rindler coordinates ##t,x##, and we have transforms $$\begin{eqnarray*}
T&=&x\sinh(\alpha t)\\
X&=&x\cosh(\alpha t)\\
x&=&\sqrt{X^2-T^2}\tag{1}\\
t&=&\frac 1\alpha\tanh^{-1}\left(\frac TX\right)\tag{2}
\end{eqnarray*}$$and a line element$$ds^2=(\alpha x)^2dt^2-dx^2$$(
Ref) First, we need to write down the trajectory of the Earth in these coordinates. In the inertial cordinates the Earth is at some fixed ##X##, say ##X=D##, for all ##T##. We can plug this into (1) and (2) and eliminate ##T## to get (
edit: after minor typo correction from @Sagittarius A-Star )$$\begin{eqnarray*}
x&=&D\sech(\alpha t)\tag{3}\\
\frac{dx}{dt}&=&-\alpha D\sech(\alpha t)\tanh(\alpha t)\tag{4}
\end{eqnarray*}$$We can then use these with the line element to get the ##ds^2## for Earth between Rindler times ##t## and ##t+dt##.$$\begin{eqnarray*}
ds^2&=&(\alpha x)^2dt^2-dx^2\\
&=&\left((\alpha x)^2-\left(\frac{dx}{dt}\right)^2\right)dt^2\\
&=&\alpha^2D^2\sech^4(\alpha t)dt^2
\end{eqnarray*}$$where we used (3) and (4) and simplified to get from the second line to the third. We can then just take the square root and integrate to get the Earth's proper time between two Rindler coordinate times, ##t_i## and ##t_f##:$$\begin{eqnarray*}
\tau&=&\int_{t=t_i}^{t_f}ds\\
&=&\alpha D\int_{t_i}^{t_f}\sech^2(\alpha t)dt\\
&=&D\left(\tanh(\alpha t_f)-\tanh(\alpha t_i)\right)\tag{5}
\end{eqnarray*}$$Finally, we need to know the ##t## coordinate when our rocket turns over and begins to decelerate. We can use the fact that turnover happens in the inertial frame at ##L/2## from the Earth, and that the Earth's ##X## coordinate is ##1/\alpha## to write the "half way" ##X## coordinate ##X_{1/2}=1/\alpha+L/2##, or ##X_{1/2}=(2+\alpha L)/2\alpha##. We know that the rocket has a constant ##x=1/\alpha##. Thus we can use (1) and (2) to write the "half way" ##T## and ##t## coordinates also:$$\begin{eqnarray*}
X_{1/2}&=&\frac{2+\alpha L}{2\alpha}\\
T_{1/2}&=&\sqrt{\frac L{4\alpha}(\alpha L+4)}\\
t_{1/2}&=&\frac 1\alpha\tanh^{-1}\left(\frac{T_{1/2}}{X_{1/2}} \right)
\end{eqnarray*}$$We now have all the pieces we need to solve this problem. We will define two Rindler coordinate systems.
The first Rindler system covers the acceleration phase. Its origin is ##1/\alpha## to the left of Earth and its ##t=0## line runs through the departure event. The Earth is "below" the rocket with ##D=D_1=1/\alpha##, and we use this coordinate system from ##t=0## to ##t=t_{1/2}##. Plugging this into (5) we find that during the acceleration phase the Earth experiences proper time ##\tau_1=D_1T_{1/2}/X_{1/2}##. Meanwhile, the rocket experienced proper time ##t_{1/2}## since its proper time matches coordinate time.
The second Rindler system covers the deceleration phase. Its origin is ##1/\alpha## to the right of Proxima and its ##x## coordinate increases to the
left. Its ##t=0## line runs through the arrival event, and (by symmetry) we use it from ##t=-t_{1/2}## to ##t=0##. In this system the Earth is "above" the rocket and has ##D=D_2=1/\alpha+L##. Again we can plug all this into (5) and find that the Earth experiences proper time ##\tau_2=D_2T_{1/2}/X_{1/2}##. Again, the rocket experienced ##t_{1/2}##.
Noting that Proxima Centauri is ##L=4.2465\mathrm{ly}## from Earth (
ref) and we want our rocket to accelerate at ##\alpha=1\mathrm{g}=1.032\mathrm{ly/y^2}##, and putting everything together$$\begin{eqnarray*}
\tau_{\mathrm{Earth}}&=&\tau_1+\tau_2\\
&=&\sqrt{\frac L\alpha(\alpha L+4)}\\
&=&5.87\mathrm{y}\\
\tau_{\mathrm{rocket}}&=&2t_{1/2}\\
&=&\frac 2\alpha\tanh^{-1}\left(\frac{\sqrt{\alpha L(\alpha L+4)}}{\alpha L+2}\right)\\
&=&3.54\mathrm{y}
\end{eqnarray*}$$This matches the OP’s calculation.