Calculate Leqv for Parallel Inductors

[Gear300]

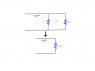
Diagram shown in attachment. Two inductors having self-inductance L1 and L2 are connected in parallel. The mutual inductance beween the two inductors is M. Determine the equivalent self-inductance Leqv for the system.

I'm pretty much stuck on this one. Since the current splits off and heads in the same direction for each inductor, the contributing emfs are in the same direction for each one but repel each others effects, so I don't think it would be a sum of the inductances. I'm not exactly sure how to take the mutual inductance into account. The answer is:
(L1*L2 - M^2)/(L1 + L2 - 2M)...any ideas?

 

[alphysicist]

Hi Gear300,

Call the current through the equivalent inductor I, and the current I1 for L1 and I2 for L2. How are these currents related? How are the derivatives of the currents with respect to time related? Then find the induced emf for all three inductors in terms of the derivatives of the currents (you'll have to choose some signs). How are these emf values related for the three inductors? At that point you can algebraically solve your system of equations for $L_{\rm eq}$.

 

[Gear300]

The mutual induction should reverse the change in current of one inductor in respect to another...

 

[alphysicist]

I believe the exact details for the signs of the emf from the mutual inductance depends on how the coils are wound. (The answer you have in your first post is not the most general formula; its for a specific way they are wound.) I don't think they give you these details, so it looks to me like you'll just need to assume a sign for the term with M and perhaps change it later if needed.

 

[Gear300]

Well...it can be deduced that since the contributed emfs repel each other, the overall inductance isn't L1 + L2, and the only other formula that commonly appears in such situations would be something like 1/L1 + 1/L2 = 1/L. Now I would have to tie mutual induction in. Since the current is heading in the same direction for each inductor, then the mutual induction should further enhance the induction in each branch. This is where things sort of distort.

1/(L1 + M) + 1/(L2 + M) = 1/L, in which L = (L1*L2 + L1*M + L2*M + M^2)/(L1 + L2 + 2M). This is not the answer I'm supposed to get...does M increase the inductance for each inductor or decrease...or does it increase for one and decrease for the other?

 

[alphysicist]

For parallel circuits we know that $I = I_1+I_2$, and so:

$$I' = I_1'+I_2'$$
where the prime means the derivative with respect to time.

Now in terms of $L_1, I_1', I_2',\mbox{ and } M$, what is the potential difference $V_1$ across $L_1$?

You can do the same for the potential difference across $L_2$ and across $L$.

Once you have those three voltage equations, you can use the fact that these are in parallel to find out how $V_1, V_2,\mbox{ and } V$ are related. At that point, you can eliminate the derivatives of the current. What do you get?

 

[Gear300]

I got L = (2L1^2 - L1*L2 - M^2)/(L1 - L2); I assumed V1 = V2 = V

 

[alphysicist]

Gear300,

Without seeing your equations for V1, V2, and V, I can't follow what you did. What did you get for V1, V2, and V?

 

[Gear300]

Wait I actually came up with an answer: (L1*L2 - M^2)/(L1 + L2 + 2M)...its pretty much the answer I'm looking for, except for the +2M in the denominator. I was sort of thinking...because the inductors are in parallel, the currents are parallel, not antiparallel to each other. Wouldn't a valid answer be with +2M?

 

[alphysicist]

The general expression is:

$$\frac{1}{L_{\rm eq}} = \frac{1}{L_1 \pm M} + \frac{1}{L_2 \pm M}$$

where the sign depends on how the windings are oriented with respect to each other. But to get the answer that you reported, I used the defined signs for the induced voltages that they give in the book:

$$V_1 = - L_1 \frac{dI_1}{dt} - M \frac{dI_2}{dt}$$

and so on.