Calculate new height of truncated cone

[tjosan]

Hi,

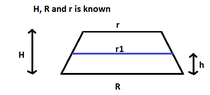
Suppose you have a truncated cone filled water with the lower radius being R, and upper r (R>r), and the height is H.

R, r and H is known so the volume, V, can be calculated using V=1/3*pi*H*(R^2+R*r+r^2). Now suppose you remove some water so that you end up with a lower volume, V1.

The water surface will now have a radius of r1, and the height will be h. The overall shape of the cone will remain the same though, its just that the surface has moved down.

How can I calculate the new height? I cannot wrap my head around this. First I just used the new volume in the formula above and solved for H, but then I realized the upper radius isn't the same anymore, so that wont work.

I attached an image to illustrate.

Thanks!

 

[Dr Transport]

think about how the radius of the cone changes with height.

 

[tjosan]

think about how the radius of the cone changes with height.

I think I solved it.

The ratio, C, between the H and R-r must remain the same for the new cone (because the angle is the same, tan (angle) = constant) , so C = H/(R-r) = H1/(R-r1) => H1=C*(R-r1) [1]

V1=1/3*pi*H1*(R^2+R*r1+r1^2) = 1/3*pi*C*(R-r1)*(R^2+R*r1+r1^2), where r1 is the new upper radius, V1 is the new volume. Solve for r1 and then use equation [1] to solve for H1.

 

[Steve4Physics]

The ratio, C, between the H and R-r must remain the same for the new cone (because the angle is the same, tan (angle) = constant) , so C = H/(R-r) = H1/(R-r1) => H1=C*(R-r1) [1]

V1=1/3*pi*H1*(R^2+R*r1+r1^2) = 1/3*pi*C*(R-r1)*(R^2+R*r1+r1^2), where r1 is the new upper radius, V1 is the new volume. Solve for r1 and then use equation [1] to solve for H1.

Your method should work (I haven’t tried it) but it looks like you will end-up having to solve a really messy cubic equation in $r_1$.

Here are some hints for an alternative approach.

With conventional notation, the volume of a cone is $V(r, h) = \frac 13 \pi r^2 h$. The difficulty here is that $V$ is a function of 2 variables, $r$ and $h$. In your question, the cone angle is effectively given; this gives a simple relationship between $r$ and $h$. You should be able to show that $V(h) = kh^3$ where $k$ is a constant. $V(h)$ is now a sinple function of the single variable $h$.

(You have enough information to find $k$ and the height of the ‘full’ cone in terms of the given data.)

The required frustum is the part of a full cone which remains after the cone’s ‘tip’ (itself a cone) is removed. $V_{frustum} = V_{full cone}~-~V_{tip}$.

Using the above gives a more manageable way to find '$h_1$'. But it’s still a bit messy.

(Note. We prefer LaTeX for equations here. The link to a guide is https://www.physicsforums.com/help/latexhelp/). This is the link shown at the bottom left of the edit window.)