Electric resistance in the truncated rotating cone

[ciso112]

Homework Statement

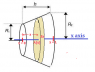
Homogeneous body with the shape of a truncated rotating cone has a base shaped like a

circle. The radius of the lower base is R2 = 8 cm and radius of the upper base is R1 =

4 cm. The height h = 8 cm (see figure). Calculate the total electric

resistance between the base surfaces of the body, when made of a material of

resistivity ρ = 4*10 ^(-2) Ohm*m. Assume that during the transport of electric charge

through the body volume, the current density changes.

Homework Equations

see the picture

The Attempt at a Solution

idea:
triple integration..one through the height...and the remaining ones through the radius and the perimeter...but does this take into account the changing of the radius at different heights?

 

[TSny]

Only a single integration is needed. Hint: thin circular disks.

 

[cnh1995]

Write a general expression for any intermediate radius in terms of R1,R2 and h. Use it for calculation of resistance of thin circular discs and integrate along proper path.

 

[ciso112]

Only a single integration is needed. Hint: thin circular disks.

hm, this gives me the integral of PI*r^2 with boundries of R2 and R1...?

 

[TSny]

hm, this gives me the integral of PI*r^2 with boundries of R2 and R1...?

This is not what you need to integrate. The entire truncated cone can be thought of as made of many thin slices (circular disks). Each disk will have a small resistance dR that will depend on the radius and thickness of the disk. These resistances are in "series", so the total resistance is the sum (or integral) of the individual resistances.

 

[cnh1995]

As you can see the resistances are in series, your limits of integration will be from 0 to h. Try writing a general expression for intermediate radius in terms of R1, R2 and h.

 

[ciso112]

intermediate radius

could you clarify this term pls, not even google helped me

 

[ciso112]

This is not what you need to integrate. The entire truncated cone can be thought of as made of many thin slices (circular disks). Each disk will have a small resistance dR that will depend on the radius and thickness of the disk. These resistances are in "series", so the total resistance is the sum (or integral) of the individual resistances.

am I getting closer? dR = (PI*r^2*dh)/dI where I is electric current

 

[cnh1995]

could you clarify this term pls, not even google helped me

The radius varies from x=0 to x=h. You need to find a general expression for radius at a distance x in terms of R1, R2 and h. That's what I meant by intermediate radius. Limits of x will be from 0 to h when you'll integrate.

 

[cnh1995]

am I getting closer? dR = (PI*r^2*dh)/dI where I is electric current

There's no need to involve current.

 

[cnh1995]

R=ρ*l/A.. For a small disc at a distance x from the leftmost end, what is the length and area of cross section in terms of x?

 

[TSny]

In the figure below, you see a disk located at position x along the axis of the cone. The disk has a thickness dx and an area A(x) which depends on x. ( You will need to express A(x) explicitly in terms of the position x.) How would you express the resistance, dR, of the disk in terms of A(x) and dx?

 

[cnh1995]

R=ρ*l/A.. For a small disc at a distance x from the leftmost end, what is the length and area of cross section in terms of x?

Radius varies linearly with x. At x=0, r=R1 and at x=h, r=R2. Using this data, can you write a general expression for r in terms of x?

 

[ciso112]

Radius varies linearly with x. At x=0, r=R1 and at x=h, r=R2. Using this data, can you write a general expression for r in terms of x?

The concept behind seems to be clear, the second thing is to write it down...what about: ...l (radius of a given element) = r1 + ((r2-r1)/h)*x

 

[cnh1995]

The concept behind seems to be clear, the second thing is to write it down...what about: l (radius of a given element) = R1 + (R2-R1 +dh) ...where dh could be x

It's like a straight line passing through (0, R1) and (h, R2). How will you write r as a function of x from this data? It is in the form r=ax+b.. Now a and b can be found using known quantities R1, R2 and h.

 

[ciso112]

It's like a straight line passing through (0, R1) and (h, R2). How will you write r as a function of x from this data? It is in the form r=ax+b.. Now a and b can be found using known quantities R1, R2 and h.

r1 + ((r2-r1)/h)*x could it be?

 

[ciso112]

In the figure below, you see a disk located at position x along the axis of the cone. The disk has a thickness dx and an area A(x) which depends on x. ( You will need to express A(x) explicitly in terms of the position x.) How would you express the resistance, dR, of the disk in terms of A(x) and dx?

dR = ρ * (r1 + (((r2-r1)/h)*x)/dA) ?

 

[cnh1995]

r1 + ((r2-r1)/h)*x could it be?

Right!

 

[ciso112]

Right!

great, I thank you so much!
now all I need is to express dA and then I can turn to mathematics, yes?

what about, dA = PI*r^2*dx?

 

[cnh1995]

dR = ρ * (r1 + (((r2-r1)/h)*x)/dA) ?

The expression you got is for radius r.
R=ρ*l/A..

 

[cnh1995]

Look at Tsny's image carefully. You need to express dR in terms of dx and A(x)..

 

[cnh1995]

r1 + ((r2-r1)/h)*x could it be?

You now know radius r as a function of x. For a small disc of resistance dR, what is the thickness and cross sectional area in terms of x? Once you get that expression, all you need to do is integrate it between 0 to h.

 

[ciso112]

Look at Tsny's image carefully. You need to express dR in terms of dx and A(x)..

I am not sure what "l" is, I think this is tha last think that needs clarification

 

[ciso112]

You now know radius r as a function of x. For a small disc of resistance dR, what is the thickness and cross sectional area in terms of x? Once you get that expression, all you need to do is integrate it between 0 to h.

if "l" is the width, then: dR = RO*(dx/PI*r^2) where r = r1 + ((r2-r1)/h)*x ?

 

[cnh1995]

if "l" is the width, then: dR = RO*(dx/PI*r^2) where r = r1 + ((r2-r1)/h)*x ?

There you go!

 

[ciso112]

There you go!

wow, words can hardly express the gratitude I feel towards you guys. Please, have all my likes
...and a video of a gopro camera set on a rocket which flies to space :D