Hi
@nao113. You haven't actually asked a question! But a few thoughts anyway….
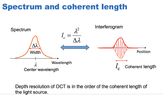
Is Δλ the FWHM (full width at half maximum) or the half-width? Let’s assume it is the FWHM.
The coherence (not ‘coherent’) length, L, In a medium of refractive index 1 is given by:
##L = C \frac {λ^2}{Δλ}##
e.g. see
https://en.wikipedia.org/wiki/Coherence_length
You have taken C=1 but typically C≈ ½. See above link.
You have been given data to 2 significant figures but your final answer has 6 significant figures - lose 1 mark in an exam’!