Lotto
- 253
- 16
- Homework Statement
- The thin, circular convex lens is placed in an opaque bracket perpendicular to the optical axis. Behind the lens is build a shade perpendicular to the optical axis at a distance ##l##. By placing a spot light source in the subject focus of the lens, a circle of light with a diameter of ##D## is formed on the shade. Moving the point source within twice the distance of the lens creates a circle of a diameter ##d##. Detrmine a focal length of the lens.
- Relevant Equations
- ##\frac{1}{2f}+\frac{1}{L}=\frac 1f##
My picture is here:
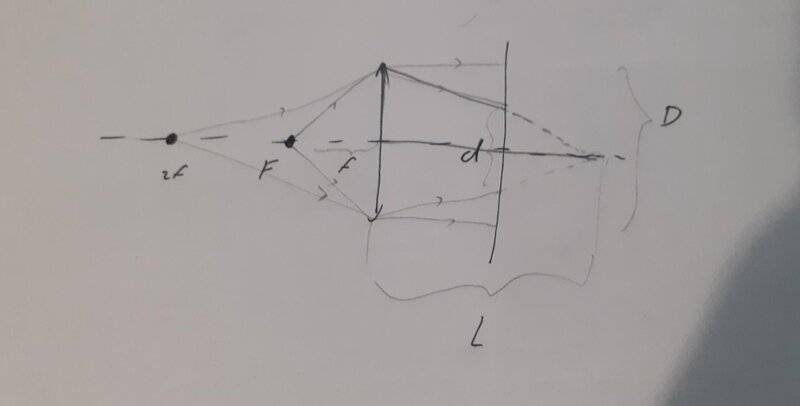
The diameter ##D## is also a diameter of the lens.
If there was no shade, the image of the moved source would be by using ##\frac{1}{2f}+\frac{1}{L}=\frac 1f## at a distance ##L=2f##. So by using a triangle similarity we get
##\frac{D/2}{L}=\frac{d/2}{L-l}##,
so ##f=\frac{Dl}{2(D-d)}##.
Is it correct?
The diameter ##D## is also a diameter of the lens.
If there was no shade, the image of the moved source would be by using ##\frac{1}{2f}+\frac{1}{L}=\frac 1f## at a distance ##L=2f##. So by using a triangle similarity we get
##\frac{D/2}{L}=\frac{d/2}{L-l}##,
so ##f=\frac{Dl}{2(D-d)}##.
Is it correct?