SUMMARY
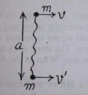
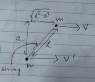
The discussion focuses on calculating the impulse of tension in a system involving two masses and a string. The impulse is defined by the equation J (Impulse) = Δ(mv) = F × Δ(t). Participants emphasize the importance of analyzing the system's motion after the string becomes taut and applying conservation laws, particularly conservation of momentum. The conversation highlights the necessity of breaking down velocity components and understanding the center of mass dynamics to solve the problem effectively.
PREREQUISITES
- Understanding of impulse and momentum concepts in mechanics
- Familiarity with Newton's laws of motion
- Knowledge of center of mass calculations
- Ability to analyze motion in orthogonal components
NEXT STEPS
- Study the application of conservation of momentum in systems with constraints
- Learn about impulse-momentum theorem in detail
- Explore the dynamics of collisions and tension in strings
- Research the concept of center of mass in multi-body systems
USEFUL FOR
Students of physics, particularly those studying mechanics, as well as educators and anyone involved in solving problems related to impulse and tension in physical systems.