Calculate the impulse of tension

[Amitayas Banerjee]

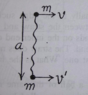
Homework Statement

Homework Equations

$$
J \space (\text{Impulse})= \Delta (mv) = F \times \Delta (t)
$$

The Attempt at a Solution

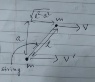
As much I interpreted, we have to calculate the impulse caused by the tension till the relative velocity of approach along the string becomes 0. T to this, I need to figure out how the system moves after the string becomes taut. I have no idea how to do that.

 

[Cutter Ketch]

Well, you’re right, you will need to have an idea of how the system moves after the collision. Try thinking about it in the center of mass coordinates. That should give you an idea.

 

[haruspex]

how the system moves after the string becomes taut.

Think about components of velocity along and normal to the string. What can you about each after it becomes taut? What conservation law can you apply?

 

[Amitayas Banerjee]

I think this is the scene just when the string becomes taut. Should I now break the velocities into orthogonal components? I can not figure out any conservation law to apply. Please help.

 

[haruspex]

Should I now break the velocities into orthogonal components?

Yes.

What conservation laws do you know for mechanics? Which might apply here?

 

[Amitayas Banerjee]

Should I conserve momentum along the string? But how can I? The string prevents a free movement along it, but I can only conserve momentum along an axis which allows free movement along it.

 

[Chestermiller]

Going back to post #2 by @Cutter Ketch . What are the velocity components of the center of mass before the string becomes taut? What are the velocity components of the center of mass after the string becomes taut? At the moment that the string gets taut, where is the center of mass located? What is the movement of each of the masses relative to the center of mass after the string becomes taut?

 

[Cutter Ketch]

Should I conserve momentum along the string? But how can I? The string prevents a free movement along it, but I can only conserve momentum along an axis which allows free movement along it.

When to conserve momentum: by Newton’s first law an object will continue in its state of motion unless acted on by a force.

Is m1 acted on by a force external to m1? Yes. Is m2 acted on by a force external to m2? Yes. Is the string acted on by a force outside the string? Yes. BUT as a whole is the system of m1, m2, and the string acted on by a force outside that system? No! So what momentum is conserved? (and don’t forget linear and angular)

 

[haruspex]

Should I conserve momentum along the string? But how can I? The string prevents a free movement along it, but I can only conserve momentum along an axis which allows free movement along it.

As @Cutter Ketch points out in post #8, you can take two masses and string as the system and apply conservation of momentum along the string. Alternatively, you can introduce an unknown impulse along the string and consider momentum of each mass separately. Indeed, you will need the second approach when considering momentum normal to the string.