chwala
Gold Member
- 2,828
- 420
- Homework Statement
- See attached.
- Relevant Equations
- Spearman's rank correlation coefficient.
Find the problem and solution here; I am refreshing on this topic of Correlation.
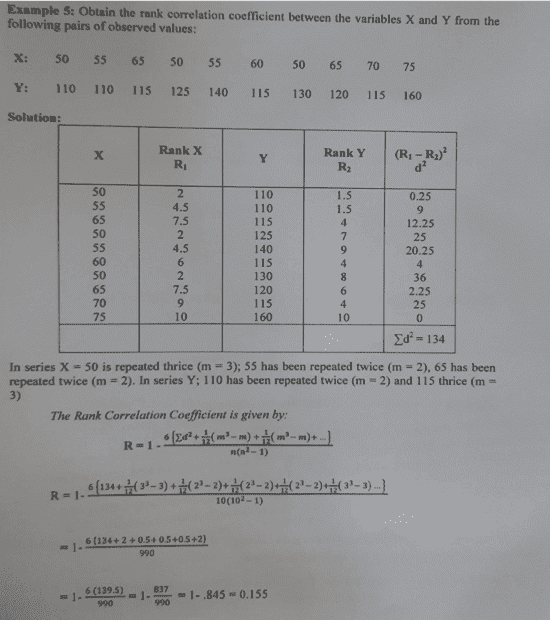
The steps are pretty much clear..my question is on the given formula ##\textbf{R}##. Is it a generally and widely accepted formula or is it some form of improvised formula approach for repeated entries/data? How did they arrive at... ##m^3-m?## ... Any proofs? Supposing ##9## entries are repeated and ##1## entry is different would the formula still hold?
Are there other different ways of solving this particular problem?
Cheers...
The steps are pretty much clear..my question is on the given formula ##\textbf{R}##. Is it a generally and widely accepted formula or is it some form of improvised formula approach for repeated entries/data? How did they arrive at... ##m^3-m?## ... Any proofs? Supposing ##9## entries are repeated and ##1## entry is different would the formula still hold?
Are there other different ways of solving this particular problem?
Cheers...
Last edited: