Calculate the sag (deflection) of a membrane

[dykuma]

Homework Statement

Not sure if this is the appropriate place to ask this question, but I didn't know where else to ask.

Anyway.

Let's assume that I have a film (or membrane) material that is stretched over some boundary, (lets assume a thin hollow cylinder). Then some constant force is applied over the surface (a pressure). Assuming the deflection is small, what is the sagitta (or depth) that the membrane is deflected by for a give material?

Homework Equations

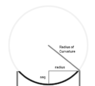
In this case, I've made several assumptions. First, the deflected part of the membrane is actually a very tiny slice of a sphere. As such, for small deflections I'm able to treat one surface of the membrane like the inside of a bubble (specifically the concave side of the deflection).

As such, my equations are:

Where P is some difference of pressure on either side of the membrane, Rc is the radius of curvatures, r is the radius (or half the span) of the un-deflected membrane,

For my purposes, I have no need to solve for the "sag" at the moment, as that information is encapsulated in the radius of curvature and can be easily calculated.

The Attempt at a Solution

Obviously, with the conditions I have set, the solution to the problem is:

Anyway, the issue I am having is being able to solve this for a specific material. From what I understand, T is the surface tension of the material, but I am not sure this is always available. My guess was that:

T=E⋅t

where E is the Young's modulus, and t is the thickness of the material. However, I am not sure that is correct.

This issue is further complicated when I assume that some form of tension is already being applies to the membrane in order to stretch it. Do I need to take that into account as well?

Basically, my question is, if I have the produce sheet of a given material (like a rubber sheet), how do I obtain the value for T?

 

[haruspex]

where E is the Young's modulus, and t is the thickness of the material

No, that's not how surface tension works. It really is a force within the surface, so is unrelated to the thickness, and quite distinct from Young's modulus.

 

[haruspex]

This issue is further complicated when I assume that some form of tension is already being applies to the membrane in order to stretch it. Do I need to take that into account as well?

No. You cannot apply additional tensions. The surface would simply stretch (without any increase in tension) to reach the wider range. It is not like elastic. The tension is entirely dictated by surface tension.

 

[Orodruin]

The surface will not be spherical in shape. For small deviations the surface deviation is going to satisfy Poisson’s equation, which is a second order differential equation. I would not call this an introductory physics problem.

 

[dykuma]

No, that's not how surface tension works. It really is a force within the surface, so is unrelated to the thickness, and quite distinct from Young's modulus.

I figured. So the surface tension is a separate property then. Is there a name that this property commonly goes by (besides surface tension)?

No. You cannot apply additional tensions. The surface would simply stretch (without any increase in tension) to reach the wider range. It is not like elastic. The tension is entirely dictated by surface tension.

So the surface tension is entirely separate from any horizontal tensions I might use to "flatten" out the membrane under a pressure that previously deformed it. I was afraid that was true too. Where would I take such a situation under consideration then?

Thinking about it, I feel like stretching it would increase the overall restoring force over the membrane (naively thinking of this like a hooke's law problem). Is this true.

The surface will not be spherical in shape. For small deviations the surface deviation is going to satisfy Poisson’s equation, which is a second order differential equation. I would not call this an introductory physics problem.

I felt that it might have been an introductory problem given the assumptions made. I also know that the shape of the deformation will not be a sphere (I believe that the actual shape should be something like a catenary), but for very small deflections (much smaller than my very exaggerated image), it should be very close to a sphere, no? For me to answer my question, should I just go for solving Poisson's equation instead?

 

[haruspex]

I feel like stretching it would increase the overall restoring force over the membrane (naively thinking of this like a hooke's law problem). Is this true.

No, as I wrote, it is not like an elastic membrane. Suppose you have it as a flat rectangle bounded by four wires. If you slide a pair of wires apart or together the membrane will get correspondingly thinner or thicker, but the tension will not change.

 

[haruspex]

The surface will not be spherical in shape.

It is given as stretched over the end of a cylinder and we are ignoring gravity. The pressure difference is the same at all parts of the membrane, and that dictates the local product of curvatures. By symmetry, would it not be spherical?

 

[Orodruin]

It is given as stretched over the end of a cylinder and we are ignoring gravity. The pressure difference is the same at all parts of the membrane, and that dictates the local product of curvatures. By symmetry, would it not be spherical?

Yes. Sometimes I think too fast for my own good.