Calculate the torsion of a silver thread

[AlejandreBurgues908]

Homework Statement

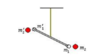
The torsion balance shown in the figure consists of a 40 cm long bar with lead balls with a diameter of 2 cm on each end. The rod is hanging by a 100 cm long silver thread with a diameter of 0.5 mm. When two bigger lead balls (density = 11.4 g/cm3) with a diameter of 30 cm are placed very close to each one of the balls, on opposite sides, their gravitational attraction tend to make the rod rotate in the same direction. What will the silver thread torsion be?

Homework Equations

F=[/B]G.m1.m2/r^2
T=r.F
Shear modulus

The Attempt at a Solution

The answer is θ = 0,00422º, but I don't know how to solve it.

 

[haruspex]

Relevant equations

What equations do you know relating masses to gravitational attraction and forces to torques?
Do you know how torsion is defined?

 

[AlejandreBurgues908]

What equations do you know relating masses to gravitational attraction and forces to torques?
Do you know how torsion is defined?

I am kinda lost, honestly is the hardest question I ever had, right now we were learning about elasticity, Young's modulus and Poisson's modulus. This is the kind of stuff we are learning (is in spanish):
http://repositorio.pucp.edu.pe/inde...56789/7140/Medina_Fisica2_Cap1.pdf?sequence=2

 

[haruspex]

I am kinda lost, honestly is the hardest question I ever had, right now we were learning about elasticity, Young's modulus and Poisson's modulus. This is the kind of stuff we are learning (is in spanish):
http://repositorio.pucp.edu.pe/inde...56789/7140/Medina_Fisica2_Cap1.pdf?sequence=2

The questions I asked are much easier though. Please try to answer them.

 

[AlejandreBurgues908]

What equations do you know relating masses to gravitational attraction and forces to torques?
Do you know how torsion is defined?

By the way I do know how the torsion is defined

 

[haruspex]

By the way I do know how the torsion is defined

So post that.

 

[AlejandreBurgues908]

So post that.

Ok

 

[Chestermiller]

Do you know how to determine the force on each ball? Do you know how to determine the moment of a force?

 

[AlejandreBurgues908]

Do you know how to determine the force on each ball? Do you know how to determine the moment of a force?

Yes, I know

 

[Chestermiller]

OK. What is the sum of the moments caused by the gravitational forces on the rod?

 

[AlejandreBurgues908]

OK. What is the sum of the moments caused by the gravitational forces on the rod?

I don't Know if this solution to your question is fine T=(2*0.2)G*m1*m2/(r1+r2)^2

 

[Chestermiller]

I don't Know if this solution to your question is fine T=(2*0.2)G*m1*m2/(r1+r2)^2

Yes. Very nice. Now, if the system is in equilibrium, the string has to apply an equal and opposite torque to the rod. This torque is determined by the elastic properties and geometry of the string, and the amount that one end of the string rotates relative to the other end. For the analysis in your textbook on how to determine the angle of rotation, see Example 43 on pages 23-24.

Incidentally, your textbook is done very well. I like it a lot.

 

[AlejandreBurgues908]

Yes. Very nice. Now, if the system is in equilibrium, the string has to apply an equal and opposite torque to the rod. This torque is determined by the elastic properties and geometry of the string, and the amount that one end of the string rotates relative to the other end. For the analysis in your textbook on how to determine the angle of rotation, see Example 43 on pages 23-24.

Incidentally, your textbook is done very well. I like it a lot.

Ok, now I understand the problem, the solution would be θ=2*T*L/(π*G*R^4) where T=(2*0.2)G*m1*m2/(r1+r2)^2 L is the lenght, R the radius and G the shear modulus, but how to calculate θ if the problem doesn't give me G?

 

[haruspex]

By the way I do know how the torsion is defined

The reason I asked is that I do not know how "torsion", as a quantity, is defined. What I can find on the net is most unclear.
At https://en.wikipedia.org/wiki/Torsion_(mechanics) I learn that its dimension is the same as that of pressure,

"Torsion is expressed in either the Pascal (Pa) ..."​

but nowhere in the equations does it indicate what constitutes the torsion:

where:

• T is the applied torque or moment of torsion in Nm.
• 
  is the maximum shear stress at the outer surface
• J_T is the torsion constant for the section. It is almost equal to the second moment of area about the neutral axis.
• r (tau) is the distance between the rotational axis and the farthest point in the section (at the outer surface).
• ℓ is the length of the object the torque is being applied to or over.
• φ (phi) is the angle of twist in radians.
• G is the shear modulus, also called the modulus of rigidity, and is usually given in gigapascals (GPa)
• The product J_TG is called the torsional rigidity wT.

Based on the dimensionality, I would guess that the torsion is $\frac{Tl}{J_T}$. For a cylinder, $J_T=\frac \pi 2r^4$.
If that is correct, you do not need to know the shear modulus. You would only need to know that if you had to find the angle of twist.

Edit: just noticed you later added the book answer as an angle, so it seems there is not universal agreement on the definition of torsion.

 

[Chestermiller]

Ok, now I understand the problem, the solution would be θ=2*T*L/(π*G*R^4) where T=(2*0.2)G*m1*m2/(r1+r2)^2 L is the lenght, R the radius and G the shear modulus, but how to calculate θ if the problem doesn't give me G?

You need to look up the young’s modulus and poisson ratio for silver, and use these to calculate G. The equation is given in your book.

 

[AlejandreBurgues908]

You need to look up the young’s modulus and poisson ratio for silver, and use these to calculate G. The equation is given in your book.

Got it, thank you very much for your help

 

[Chestermiller]

The reason I asked is that I do not know how "torsion", as a quantity, is defined. What I can find on the net is most unclear.
At https://en.wikipedia.org/wiki/Torsion_(mechanics) I learn that its dimension is the same as that of pressure,

"Torsion is expressed in either the Pascal (Pa) ..."​

but nowhere in the equations does it indicate what constitutes the torsion:

where:

• T is the applied torque or moment of torsion in Nm.
• 
  is the maximum shear stress at the outer surface
• J_T is the torsion constant for the section. It is almost equal to the second moment of area about the neutral axis.
• r (tau) is the distance between the rotational axis and the farthest point in the section (at the outer surface).
• ℓ is the length of the object the torque is being applied to or over.
• φ (phi) is the angle of twist in radians.
• G is the shear modulus, also called the modulus of rigidity, and is usually given in gigapascals (GPa)
• The product J_TG is called the torsional rigidity wT.

Based on the dimensionality, I would guess that the torsion is $\frac{Tl}{J_T}$. For a cylinder, $J_T=\frac \pi 2r^4$.
If that is correct, you do not need to know the shear modulus. You would only need to know that if you had to find the angle of twist.

Edit: just noticed you later added the book answer as an angle, so it seems there is not universal agreement on the definition of torsion.

Something is wrong with the wiki article saying that torsion has units of Pa. Later it says Nm, which is correct. The torsion per unit volume has units of Pa. I always use torsion and moment as synonyms.

 

[haruspex]

Something is wrong with the wiki article saying that torsion has units of Pa. Later it says Nm, which is correct. The torsion per unit volume has units of Pa. I always use torsion and moment as synonyms.

Ok, thanks.
Strange that I could not find any reference that defined such a quantity. All the others only used 'torsion' in an abstract sense, naming the topic rather than a quantity.
Do you know if that textbook defines it?

 

[Chestermiller]

Ok, thanks.
Strange that I could not find any reference that defined such a quantity. All the others only used 'torsion' in an abstract sense, naming the topic rather than a quantity.
Do you know if that textbook defines it?

Are you referring to the OP's textbook? I can't answer this because the book is in Spanish.

 

[haruspex]

Are you referring to the OP's textbook? I can't answer this because the book is in Spanish.

From your comment in post #12 I thought you might have access to a copy. But I guess you were just basing it on the link provided.

Edit:
I just Google-translated the doc at the link. The translation does not use the word "torsion", let alone define it.
Presumably the question is not from the textbook. Maybe it comes down to the OP's translation of the actual question.

 

[AlejandreBurgues908]

From your comment in post #12 I thought you might have access to a copy. But I guess you were just basing it on the link provided.

Edit:
I just Google-translated the doc at the link. The translation does not use the word "torsion", let alone define it.
Presumably the question is not from the textbook. Maybe it comes down to the OP's translation of the actual question.

Torsion in Spanish is also torsión, maybe Google translated to twist or something related, and isn't a real book, is just a PDF with some exercises that my teacher used as examples, the exercise 43 basically defines torsion but It doesn´t say the units.

 

[Tom.G]

Google translate to the rescue again!

If you look at Example 44 in the same paper you will see that "torsion" is sometimes used where "twist" would be used in English.

Also Example 44 shows how to calculate the twist (torsion) angle for a solid cylinder.

Cheers,
Tom