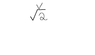Calculate the velocity of a body with twice the mass to have the same KE

[Richie Smash]

Homework Statement

A body of mass m, moves with a velocity v, and has a certain kinetic energy. What velocity would a body of twice the mass have to move to have the same kinetic energy.

Homework Equations

K.E=1/2mv²

The Attempt at a Solution

I made an equation
2m₁/2*v₁²/2= m₂v₂²/2

from here I was able to calculate that
v₂²=√v₁²/4
so v₂=v/2I believe it would have to be moving at half the speed no?

But I don't know how to formulate an answer.

The correct answer is hard to describe, so I'll post a picture.

What is that symbol? I'm just copying what I see in my book, but it might just be how it comes out in print but I think it means v/(squareroot of 2)

And if so I'm thoroughly confused as to how that is the answer.

 

[kuruman]

If you have two bodies moving at different speeds, it is a good habit to use subscripts to distinguish the masses and the speeds. Try rewriting the equation using m₁, v₁ for the first mass and m₂, v₂ for the second mass.

 

[Richie Smash]

I've changed it up a bi my answer still is not the correct one, and I don't know what the method is, sigh this is frustrating

 

[kuruman]

I've changed it up a bi my answer still is not the correct one, and I don't know what the method is, sigh this is frustrating

The equation that you started from does not look right. Start with
KE₁ = ½m₁v₁² and
KE₂ = ½m₂v₂²
If body 2 has twice the mass of body 1, how would you say that with an equation?

 

[Richie Smash]

KE = 1/2(2m₁v₂²)

Which would simplify to KE₂=m₁v₂²

 

[Orodruin]

KE = 1/2(2m₁v₂²)

Which would simplify to KE₂=m₁v₂²

Now compare that to the KE of the other mass.

 

[Richie Smash]

Right so I would do

m₁v₂²= (m₁v₁²)/2

SO

V₂²= V₁²/2

V₂= V₁/√2...

Oh... right... Now I understand :/

Sorry for not seeing the obvious answer :( but thank you.

 

[Orodruin]

Sorry for not seeing the obvious answer :( but thank you.

No need to be sorry. We are happy to help regardless of whether an answer is obvious or requires pages of calculations.

I have gone ahead and marked this thread as solved.

 

[DLeuPel]

There is also another way of doing it which is somewhat simpler.

Ec= 2m(1)×v²(2)×½
Ec×2/2×m= v²
Ec/m = v²
v = √Ec/√m

 

[kuruman]

There is also another way of doing it which is somewhat simpler.

Ec= 2m×v²×½
Ec×2×m/2= v²
Ec×m = v²
v = √Ec/√m

Is this an answer to the original question? When you write Ec= 2m×v²×½, Ec is the KE of the body 2 and v is the speed of body 2 not the given speed v of body 1. So all you have done is push symbols around the equation for the KE of body 2 without finding how the speed of body 2 is related to the speed of body 1.

 

[DLeuPel]

Is this an answer to the original question? When you write Ec= 2m×v²×½, Ec is the KE of the body 2 and v is the speed of body 2 not the given speed v of body 1. So all you have done is push symbols around the equation for the KE of body 2 without finding how the speed of body 2 is related to the speed of body 1.

Ec ( KE of both bodies) =
2xm(1) x v^2 (2) x 1/2
It is an answer to the original question but without having to find the relationship between them. Although I should have specified what velocities and mases I was talking of.
Good day

 

[Orodruin]

Ec ( KE of both bodies) =
2xm(1) x v^2 (2) x 1/2
It is an answer to the original question but without having to find the relationship between them. Although I should have specified what velocities and mases I was talking of.
Good day

The entire point of the exercise was to express the velocity of one in the velocity of the other ...

 

[DLeuPel]

The entire point of the exercise was to express the velocity of one in the velocity of the other ...

That is not stated in the given problem. I just posted another way to solve this exercise in a way which results much more simpler than the method that other users have posted.

 

[Orodruin]

That is not stated in the given problem. I just posted another way to solve this exercise in a way which results much more simpler than the method that other users have posted.

Yes it is. You have the mass and the velocity of the original body.

A body of mass m, moves with a velocity v, and has a certain kinetic energy.

You do not have the kinetic energy. It is just stated that the body will have a particular kinetic energy. Regardless, your way is really no different from what has already been presented in this thread. The only difference is that you have not done the algebra to find the relationship between the velocities.

 

[DLeuPel]

Yes it is. You have the mass and the velocity of the original body.

You do not have the kinetic energy. It is just stated that the body will have a particular kinetic energy. Regardless, your way is really no different from what has already been presented in this thread. The only difference is that you have not done the algebra to find the relationship between the velocities.

The only thing the problem asks is the v that it would have if the mass would be double. Just read the problem and it answers for itself.

 

[Orodruin]

The only thing the problem asks is the v that it would have if the mass would be double. Just read the problem and it answers for itself.

I am sorry, but it is quite obvious from the problem formulation what the given knowns are and that the kinetic energy is not one of them other than in terms of its expression in the mass and velocity. Besides, as already stated, "your" approach is really no different from what has already been presented here.

 

[DLeuPel]

I am sorry, but it is quite obvious from the problem formulation what the given knowns are and that the kinetic energy is not one of them other than in terms of its expression in the mass and velocity. Besides, as already stated, "your" approach is really no different from what has already been presented here.

I forgive you

 

[kuruman]

The only thing the problem asks is the v that it would have if the mass would be double. Just read the problem and it answers for itself.

Physics questions have certain implicit conventions when they are formulated. Some pieces of information are explicitly stated while others are not. For example, in projectile motion problems it is sometimes (but not usually) stated that air resistance is to be ignored. Nevertheless, it is never stated to ignore the Coriolis force due to the Earth's rotation or the gravity pull of the Sun, the Moon and Jupiter. If everything were explicitly stated, physics problems would read like a legal document and students would spend all their time on a test reading the questions instead of thinking how to answer them.

When a question gives you $a$ and $b$ and asks you to find $x$, then the convention is that you find an expression $x= ...$ that involves only $a$ and $b$ on the right side plus the appropriate constants like $\pi$, $g$, etc. If you do not follow this convention on a test question, it will be marked incorrect so be prepared to argue the legal case to your instructor. Good luck.