Calculate velocities in COM reference frame for 2D collision

[rdemyan]

Homework Statement

Calculate velocities in COM reference frame for 2D collision

Relevant Equations

See post

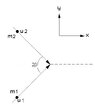
I'm trying to calculate the incoming velocities in the COM reference frame for the attached diagram. Uppercase L means laboratory frame and CM means center of mass reference frame.

1) Calculate the x and y components of the center of mass velocity

$$u_{cmx} = \frac{m_1u_1cos\beta + m_2u_2cos\beta}{m_1+m_2}$$

$$u_{cmy} = \frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1+m_2}$$

2) Calculate the velocities in the center of mass frame in the x direction and y direction

$$u_{1x}^{CM} = u_1cos\beta - u_{cmx} = u_1cos\beta - \frac{m_1u_1cos\beta + m_2u_2cos\beta}{m_1+m_2}$$

or

$$u_{1x}^{CM} = \frac{m_1u_1cos\beta+m_2u_1cos\beta -m_1u_1cos\beta - m_2u_2cos\beta}{m_1+m_2} = \frac{m_2cos\beta(u_1-u_2)}{m_1+m_2}$$

and similarly,

$$u_{2x}^{CM} = u_2cos\beta - u_{cmx} = u_2cos\beta - \frac{m_1u_1cos\beta + m_2u_2cos\beta}{m_1+m_2}$$


or

$$u_{2x}^{CM} = \frac{m_1u_2cos\beta+m_2u_2cos\beta -m_1u_1cos\beta - m_2u_2cos\beta}{m_1+m_2} = \frac{m_1cos\beta(u_2-u_1)}{m_1+m_2}$$

And in the center of mass reference frame,

$$m_1u_{1x}^{CM} + m_2u_{2x}^{CM} = 0$$

or
$$\frac{m_1m_2cos\beta(u_1-u_2)}{m_1+m_2} = -\frac{m_1m_2cos\beta(u_2-u_1)}{m_1+m_2}$$

which is verified.

However, in the y-axis reference frame, I can't get the momentums to zero out. In the y-axis,

$$u_{1y}^{CM}= u_1sin\beta - u_{cmy} = u_1sin\beta - \frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1+m_2}$$

or

$$u_{1y}^{CM} = \frac{m_1u_1sin\beta+m_2u_1sin\beta -m_1u_1sin\beta + m_2u_2sin\beta}{m_1+m_2} = \frac{m_2sin\beta(u_1+u_2)}{m_1+m_2}$$

And for the particle #2,

$$u_{2y}^{CM} = u_2sin\beta - u_{cmy} = u_2sin\beta - \frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1+m_2}$$

or

$$u_{2y}^{CM} = \frac{m_1u_2sin\beta+m_2u_2sin\beta -m_1u_1sin\beta + m_2u_2sin\beta}{m_1+m_2} = \frac{m_1sin\beta(u_2-u_1) + 2m_2u_2sin\beta}{m_1+m_2}$$

For the y-axis momentum in the zero momentum reference frame,

$$m_1u_{1y}^{CM} \neq -m_2u_{2y}^{CM} $$

I'm not sure what I am doing wrong here.

 

[haruspex]

What is the y component of particle 2’s velocity in the ground frame?

 

[rdemyan]

$$m_2u_2sin\beta$$

It is in the opposite direction of that for particle 1: $m_1u_1sin\beta$

 

[haruspex]

It is in the opposite direction of that for particle 1: $m_1u_1sin\beta$

So what sign should you have used here?

$$u_{2y}^{CM} = u_2sin\beta - u_{cmy} = u_2sin\beta - \frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1+m_2}$$

 

[rdemyan]

So what sign should you have used here?

I think I realize now that I have to think more about whether to subtract or add $u_{cm}$ to the lab frame velocity. Although the drawing doesn't show it, I am specifically assuming that the momentum $m_1u_1$ is greater than $m_2u_2$ (however, this isn't necessary, it just helps me to use the correct signs in the lab reference frame). So that means that the center of mass will move in the +y and +x directions. If I then calculate the movement of each particle in the COM frame, the particle moving upward (#1) has to have the y-component COM velocity subtracted and the particle moving downward (#2) has to have the y-component of the COM velocity added. For the x-direction, the x-component COM velocity is subtracted for both particle 1 and particle 2.

The formulas for $u_{1x}^{CM}, u_{2x}^{CM},u_{1y}^{CM}$ are correct as given in the original post. However, the formula for $u_{2y}^{CM}$ should be

$$u_{2y}^{CM} = u_2sin\beta + u_{cmy} = u_2sin\beta + \frac{m_1u_1sin\beta - m_2u_2sin\beta}{m_1+m_2}$$

which is
$$u_{2y}^{CM} = \frac{m_1u_2sin\beta+m_2u_2sin\beta + m_1u_1sin\beta -m_2u_2sin\beta}{m_1+m_2} = \frac{m_1sin\beta(u_1+u_2)}{m_1+m_2}$$

Now, in the x direction,

$$m_1u_{1x}^{CM} + m_2u_{2x}^{CM} = 0$$

but in the y-direction there should be a negative sign, shouldn't there ???

$$m_1u_{1y}^{CM} -m_2u_{2y}^{CM} = 0$$

If so, then

$$\frac{m_1m_2sin\beta(u_1+u_2)}{m_1+m_2} = \frac{m_1m_2sin\beta(u_1+u_2)}{m_1+m_2}$$

 

[erobz]

If I'm riding on the center of mass and it's moving up ( positive direction) with velocity $v_y$ the particle $m_2$ approaches me with magnitude $| v_y + u_2 \sin \beta|$ and I measure it to be negative w.r.t. the convention. So I'm seeing it as $- u_2 \sin \beta - v_y$.

 

[PeroK]

I don't understand the difficulty. For two particles we have:
$$(m_1+m_2)\vec v_{CM} =m_1\vec v_1+m_2\vec v_2$$This can be obtained by differentiating the displacement of the centre of mass:
$$\vec r_{CM} = \frac {m_1\vec r_1 + m_2\vec r_2}{m_1+m_2}$$And the velocity of particle 1 in the CM frame is:
$$\vec v'_1 = \vec v_1 - \vec v_{CM}$$The rest is just keeping track of velocity components.

 

[rdemyan]

If I'm riding on the center of mass and it's moving up ( positive direction) with velocity $v_y$ the particle $m_2$ approaches me with magnitude $| v_y + u_2 \sin \beta|$ and I measure it to be negative w.r.t. the convention. So I'm seeing it as $- u_2 \sin \beta - v_y$.

Okay, so in that case:

$$u_{2y}^{CM} = -\frac{m_1sin\beta(u_1+u_2)}{m_1+m_2}$$

and then I can use:

$$m_1u_{1y}^{CM} + m_2u_{2y}^{CM} = 0$$

and get the equality.

 

[PeroK]

PS it's worth taking the next step and calculating a general expression for the velocity of each particle in the CM frame.

 

[PeroK]

PPS you could even go back and calculate the displacement of each particle in the CM frame and differentiate that.

 

[haruspex]

I have to think more about whether to subtract or add ucm

It is a matter of being consistent about which direction is positive. If particle 1 is approaching at angle $\beta$ to the horizontal then particle 2 is approaching at angle $-\beta$. $\cos(-\beta)=\cos(\beta)$ but $\sin(-\beta)=-\sin(\beta)$.

 

[PeroK]

It is a matter of being consistent about which direction is positive. If particle 1 is approaching at angle $\beta$ to the horizontal then particle 2 is approaching at angle $-\beta$. $\cos(-\beta)=\cos(\beta)$ but $\sin(-\beta)=-\sin(\beta)$.

Unless you impose that consistency then in this case we have $\vec u_1 = \vec u_2$. Which is clearly not the case.

 

[rdemyan]

It is a matter of being consistent about which direction is positive. If particle 1 is approaching at angle $\beta$ to the horizontal then particle 2 is approaching at angle $-\beta$. $\cos(-\beta)=\cos(\beta)$ but $\sin(-\beta)=-\sin(\beta)$.

Agreed that this is something very important for me to remember. But when it comes to the direction of the center of mass, how can I know just from the equations without knowing which of the two particles has the greater momentum. If $m_1u_1 > m_2u_2$, then the COM moves upward to the right, i.e. in the positive x and positive y direction. But, if $m_1u_1 < m_2u_2$, then the COM moves downward to the right, i.e. in the positive x and negative y direction. So when I look at only equations, how do I know whether to subtract or add the components of $u_{cm}$? I guess the way to do it is to always write the calculations of the "incoming" velocities in the center of mass frame with "-" signs. For example:

$$u_{1y}^{CM} = u_1sin(+\beta) - u_{cmy}$$

$$u_{2y}^{CM} = u_2sin(-\beta) - u_{cmy}$$


If an actual numerical example is a case where $m_1u_1 < m_2u_2$, then the y component of $u_{cm}$ will be negative and the calculated values from the equations are automatically adjusted to reflect this. This general idea would also be true in the x direction.

Further, I think this means that I would always need to write the calculations of the "outgoing" velocities in the center of mass frame with "+" signs.

 

[haruspex]

how can I know just from the equations without knowing which of the two particles has the greater momentum.

You do not need to predict it. Just decide which directions you are taking as positive and write the equations consistently. The sign of the result will tell you the actual direction.

I guess the way to do it is to always write the calculations of the "incoming" velocities in the center of mass frame with "-" signs.

That is a question about relative velocities. If $\vec v$ represents the velocity of a particle in frame A and $\vec v_{BA}$ is the velocity of frame B relative to frame A (e.g. the velocity of the common mass centre here) then the velocity of the particle in frame B is $\vec v-\vec v_{BA}$.

 

[rdemyan]

It is a matter of being consistent about which direction is positive. If particle 1 is approaching at angle $\beta$ to the horizontal then particle 2 is approaching at angle $-\beta$. $\cos(-\beta)=\cos(\beta)$ but $\sin(-\beta)=-\sin(\beta)$.

You say that particle 1 is approaching at an angle of $+\beta$, but I am not sure how you determined that. Moving in a counterclockwise direction, relative to the upper right quadrant of the drawing, the angle is $180 + \beta$ for particle 1 and the angle for particle 2 is $180 - \beta$. It's not clear to me how you made the statement that you did regarding which one of the $\beta$ values is negative or positive. I'm not saying it doesn't make sense because, if one defines negative y to be in the downward direction, just looking at the directions of the y component velocities indicates that the y momentum in the downward direction is negative. But it's not clear to me how defining the upward y direction as positive means that the value of the angle in the left upward quadrant is negative while the angle in the left downward quadrant is positive.

 

[haruspex]

You say that particle 1 is approaching at an angle of $+\beta$,

No, I wrote "if", i.e. if you define the angle of approach such that particle 1's angle is $\beta$; namely, if you measure it anticlockwise from the positive x axis. If you measure it that way for particle 1 then to use the same form of equation for particle 2 you must measure its angle of approach the same way, getting $2\pi-\beta$, which is the same as $-\beta$.

 

[rdemyan]

No, I wrote "if", i.e. if you define the angle of approach such that particle 1's angle is $\beta$; namely, if you measure it anticlockwise from the positive x axis. If you measure it that way for particle 1 then to use the same form of equation for particle 2 you must measure its angle of approach the same way, getting $2\pi-\beta$, which is the same as $-\beta$.

First off, for particle 2 I don't know how you got an angle of $2\pi - \beta$ as measured from the positive x axis where the angle is equal to zero. The negative x axis would be equal to $\pi$.

Are you defining the negative axis as 0 degrees and positive increases in the angle occur in the counterclockwise direction. If so, then the angle for particle 1 is $\beta$ and for particle 2 is -$\beta$. Seems like an odd definition though. Is the definition of the the magnitude of the angle completely independent of how positive and negative is defined for the x and y axes?

 

[erobz]

First off, for particle 2 I don't know how you got an angle of $2\pi - \beta$ as measured from the positive x axis where the angle is equal to zero. The negative x axis would be equal to $\pi$. Also, I don't see how you get $2\pi - \beta = -\beta$

Assume:

$$2\pi - \beta = -\beta$$

Add $\beta$ to both sides. This results in

$$2\pi = 0$$

This is what is being said.

 

[rdemyan]

View attachment 359510

This is what is being said.

Sorry, I changed my post on you. Yes, I understand that, but my drawing is in the left hand quadrants not the right hand. This would require defining zero degrees as being the negative x axis and moving counterclockwise. I still have the question if the way to define the angles is completely arbitrary or dependent upon how positive and negative is defined for the axes?

 

[erobz]

Sorry, I changed my post on you. Yes, I understand that, but my drawing is in the left hand quadrants not the right hand. This would require defining zero degrees as being the negative x axis and moving counterclockwise. I still have the question if the way to define the angles is completely arbitrary or dependent upon how positive and negative is defined for the axes?

It doesn't matter which direction the $x$ axis is.

What is important is that if you are working in one convention, you stay consistent with that convention. What you are doing is saying clockwise is positive for one $\beta$, and counter clockwise is positive for the other $\beta$ - two conventions one problem. @haruspex are telling you to pick a single convention and stick with it for all parts of the problem and it will shake out.

 

[rdemyan]

Sorry, I changed my post on you. Yes, I understand that, but my drawing is in the left hand quadrants not the right hand. This would require defining zero degrees as being the negative x axis and moving counterclockwise. I still have the question if the way to define the angles is completely arbitrary or dependent upon how positive and negative is defined for the axes?

I guess they are interdependent. My drawing clearly shows $\beta$ in the left quadrants, so that means I have to define the negative x axis as zero degrees. Since I have defined the downward y axis as negative, that means that I have to travel counterclockwise for the angle because the only way that calculations of the y-component of the velocity vector of particle 2 are negative is if the angle that particle 2 makes with the x-axis is negative.

$$\sin(-\beta)= -sin\beta$$

 

[erobz]

I guess they are (independent). My drawing clearly shows $\beta$ in the left quadrants, so that means I have to define the negative x axis as zero degrees.

You don't "have to", you could do this if you like.

 

[rdemyan]

I'm still having some difficulty understanding how the cosine and sine of the angle will dictate whether the vector component of a velocity will point to the right or left for the x direction or upward or downward for the y direction. I like this general approach because it doesn't require that I know in exactly which direction the particles will travel after the collision. Of course, before the collision I do know the masses, velocities and the directions or angles of the collision.

I think I understand how in the left figure of the attached drawing, the angle made between the path that particle 2 takes towards the collision point is, for this example, -45 degrees (45 has to be subtracted from 180 degrees). Likewise with particle 1 the angle between its path and the x axis is +45 degrees (45 degrees has to be added to 180 degrees). For this diagram, the calculated x vectors based on the cosines of the angles are positive for both particles 1 and 2. For particle 2 the calculated y vector based on the sine of -45 degrees is negative and for particle 1 based on the sine of +45 degrees is positive. All of this agrees with the way the directions for the x and y axes have been defined.

Now assume that the particles are moving away from the collision point in the directions shown in the right figure of the drawing (and these directions are hypothetical and for illustrative purposes only). Based on the way I've defined the directions for the x and y axes and for the measurement of angles, how do I get angles A and B that when you take the cosine of these angles will lead to a negative x direction??

 

[PeroK]

Technically, you should put the origin of the x and y axes at the base of any vector. Not the tip. You then use the convention that the positive x-axis is zero degrees, the positive y-axis is 90 degrees, the negative x-axis is 180 degrees, and the negative y-axis is 270 degrees.

The line from the base to the tip of the vector has some angle, $\theta$, using this convention.

Using this convention, the components of the vector are:
$$ v_x = v\cos \theta, \ v_y = v\sin \theta$$Where $v$ is the magnitude of the vector.

 

[rdemyan]

Technically, you should put the origin of your x and y axes at the base of any vector. Not the tip. You then use the convention that the positive x-axis is zero degrees, the positive y-axis is 90 degrees, the negative x-axis is 180 degrees, and the negative y-axis is 270 degrees.

The line from the base to the tip of the vector has some angle, $\theta$ using this convention.

Using this convention, the components of your vector are:
$$ v_x = v\cos \theta, \ v_y = v\sin \theta$$Where $v$ is the magnitude of your vector.

OK. My drawings already have the angles defined as you have suggested. But typically the x and y components for a hypotenuse are determined for a right triangle. Since the right hand drawing meets your criteria, how can this yield a negative value for the x component vectors? The cosine of either positive or negative values of the same absolute angle are positive if the value of the angle is less than or equal to 90. The only way I can see getting negative values is if the angle is between 90 degrees and 270 degrees in which case the cosine is negative regardless if the angle value is positive or negative. Perhaps you are setting $\theta$ in a different way than A and B shown on the diagram?

 

[PeroK]

OK. My drawings already have the angles defined as you have suggested. But typically the x and y components for a hypotenuse are determined for a right triangle. Since the right hand drawing meets your criteria, how can this yield a negative value for the x component vectors? The cosine of either positive or negative values of the same absolute angle are positive if the value of the angle is less than or equal to 90. The only way I can see getting negative values is if the angle is between 90 degrees and 270 degrees in which case the cosine is negative regardless if the angle value is positive or negative. Perhaps you are setting $\theta$ in a different way than A and B shown on the diagram?

I don't understand much of that. I've given you the standard convention for sine and cosine. If you use that you cannot go wrong.

A sine or cosine can be negative. It depends on the quadrant. 2nd and 3rd for cosine. 3rd and 4th for sine.

 

[rdemyan]

I don't understand much of that. I've given you the standard convention for sine and cosine. If you use that you cannot go wrong.

A sine or cosine can be negative. It depends on the quadrant. 2nd and 3rd for cosine. 3rd and 4th for sine.

Could you at least show me the angle $\theta$ on my right hand drawing or define it based on my angle A in one case and angle B in the other case?

 

[PeroK]

Could you at least show me the angle $\theta$ on my right hand drawing or define it based on my angle A in one case and angle B in the other case?

Your lefthand diagram is unconventional. I think you've got yourself confused.

In your righthand diagram $\theta = 180 -A$.