A Calculate velocity of streams impinging at differing angles

[rdemyan]

TL;DR Summary

Calculate the velocity of two streams impinging upon one another where the collision is 100% elastic. After the collision, liquid flows in two different directions

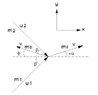
I have two streams that impinge upon one another as shown in the diagram. Stream 1 with mass flow rate of $m_1$ and velocity of $u_1$ impinges upon Stream 2 with mass flow rate of $m_2$ and velocity of $u_2$. This results in flow in the forward (f) and backward (b) direction of the x axis. $m_1, m_2, u_1, u_2$ are known. I am assuming that the collision is 100% elastic so that no energy is lost as a result of the collision. In addition, the velocity of the two streams after the collision is identical ($v$). After the collision, there are no component momentums in the y direction.

The angles of the collision of each stream, relative to the x-axis, are shown on the diagram.

I want to determine $m_f, m_b, v$. I will develop the solution for the problem below, but will now state what the issue is. The problem is that the velocity, $v$, calculated from a momentum balance does not equal $v$ calculated from an energy balance. I'm posting because I need to know if conceptually I am not looking at the modeled solution for this problem correctly.

The general strategy for the momentum balance method is to look at each stream individually and calculate the forward and backward flow for each stream independently of the other stream. Then after these quantities are calculated for each stream they are simply added together to get the quantities for the combined streams in the forward and backward direction. The velocity, $v$ is then calculated from an overall momentum balance in the x direction.

So for stream 1

$$(1)\hspace{1cm} m_1u_1\cos(\beta - \alpha) = (m_{f1} - m_{b1})v_1$$

then since $v_1 = u_1$ because no energy is lost,

$$(2)\hspace{1cm} m_{f1} - m_{b1} = m_1\cos(\beta - \alpha)$$

but since $m_1 = m_{f1} + m_{b1}$,

$$(3)\hspace{1cm} m_1 - 2m_{b1} = m_1\cos(\beta - \alpha)$$

and

$$(4)\hspace{1cm} m_{b1} = m_1\left(\frac{1-\cos(\beta - \alpha)}{2} \right)$$

Therefore

$$(5)\hspace{1cm} m_{f1} = m_1 - m_1\left(\frac{1-\cos(\beta - \alpha)}{2} \right) = m_1\left[1 - \left(\frac{1-\cos(\beta - \alpha)}{2} \right) \right]$$

or
$$(6)\hspace{1cm} m_{f1} = m_1\left(\frac{1+\cos(\beta - \alpha)}{2} \right)$$

A development for stream 2 using the same methodology yields similar equations

$$(7)\hspace{1cm} m_{b2} = m_2\left(\frac{1-\cos(\beta + \alpha)}{2} \right)$$

$$(8)\hspace{1cm} m_{f2} = m_2\left(\frac{1+\cos(\beta + \alpha)}{2} \right)$$

So, I can solve for $m_b, m_f$ as follows.

$$(9)\hspace{1cm} m_{b} =m_{b1} + m_{b2} = m_1\left(\frac{1-\cos(\beta - \alpha)}{2} \right) + m_2\left(\frac{1-\cos(\beta + \alpha)}{2} \right)$$

$$(10)\hspace{1cm} m_{f} =m_{f1} + m_{f2} = m_1\left(\frac{1+\cos(\beta - \alpha)}{2} \right) + m_2\left(\frac{1+\cos(\beta + \alpha)}{2} \right)$$

Now, if I want to calculate the velocity ($v$) of the forward and backward streams after the collision, I'm thinking I can use an overall momentum balance (i.e. for both streams) in the x direction, which is,

$$(11)\hspace{1cm} m_1u_1\cos(\beta - \alpha) +m_2u_2\cos(\beta + \alpha) = (m_f - m_b)v$$

and solving for $v$ yields,

$$(12)\hspace{1cm} v = \frac{m_1u_1\cos(\beta - \alpha) +m_2u_2\cos(\beta + \alpha)}{(m_f - m_b)} $$

All quantities are known so I can solve for $v$.

The problem is that shouldn't this solution for $v$ equal the solution obtained from an energy balance? $v$ can be calculated from an energy balance as follows (no energy lost as a result of the collision or anything else),

$$(13)\hspace{1cm} \frac{m_1 u_1^2}{2} + \frac{m_2 u_2^2}{2} = \frac{m_f v^2}{2} + \frac{m_b v^2}{2}$$


and solving for $v$ yields,
$$(14)\hspace{1cm} v = \sqrt{\frac{m_1 u_1^2 + m_2 u_2^2}{m_1+m_2}}$$

When I plug in numbers, $v$ calculated from Eq. 12 does not equal $v$ calculated from Eq. 14. Yet, they should be equal. So, I must be making a mistake or not understanding something conceptually. Any help is appreciated.

 

[Philip Koeck]

TL;DR Summary: Calculate the velocity of two streams impinging upon one another where the collision is 100% elastic. After the collision, liquid flows in two different directions

I would say the final directions are incompatible with elastic particle collisions.
I wouldn't assume that macroscopic energy is conserved.

 

[A.T.]

I would say the final directions are incompatible with elastic particle collisions.
I wouldn't assume that macroscopic energy is conserved.

Yes, fully elastic collision would mean that the streams bounce back along the y-axis, not join and move only along x-axis after the collision.

 

[rdemyan]

I

I would say the final directions are incompatible with elastic particle collisions.
I wouldn't assume that macroscopic energy is conserved.

In reality energy is not conserved. This is a hypothetical case, which I am using as a sort of control for eventual implementation of my theories of how energy is dissipated as a result of the collision.

With regards to the final directions after the collision, this has been something that has stumped me a bit. The drawing that I showed in the post is a rotation of the actual physical situation - hence the angles $\beta - \alpha$ and $\beta + \alpha$. The issue is with what happens to the backward flowing stream. The first diagram attached above shows a case where the momentum of stream 1 is greater than that of stream 2 and the streams impinge at an angle of 2$\beta$. I simply rotated this first diagram to come up with the diagram I showed in the original post. As you can see in the diagram before rotation, $m_b$ points downwards at an angle of $-\alpha$, which is something I am doubting is correct. If it points down, I can readily solve the momentum equations because the overall y momentum balance (not shown in the original post), allows me to calculate $\alpha$. If it points up at the same angle as $m_f$, namely $+\alpha$, then solution is more difficult (see the second diagram above attached to this reply).

However, I think you are right about the directions after the collision. I think $m_b$ needs to point in the same direction as $m_f$ (depending upon which of the incoming streams has the greater momentum) prior to any rotation of the diagram. I will work on revising the equations today, but I suspect I will now have a problem solving for $\alpha$.

 

[A.T.]

Yes, fully elastic collision would mean that the streams bounce back along the y-axis, not join and move only along x-axis after the collision.

After thinking about it, I don't think the above required.

All is required to have energy conserved is that each stream is split in two parts, each part is then deflected without speed loss and recombines with one of the parts of the other intial stream that is deflected in the same direction.

 

[rdemyan]

After thinking about it, I don't think the above required.

All is required to have energy conserved is that each stream is split in two parts, each part is then deflected without speed loss and recombines with one of the parts of the other intial stream that is deflected in the same direction.

Yes. If I understand you correctly that is what I was trying to do in my original post. But I'm thinking that maybe my diagram in the original post is not correct. I'm currently working on the equations for the 2nd diagram in my 1st reply post. Do you think that that second diagram is correct assuming that the momentum of incoming stream 1 is greater than the momentum of incoming stream 2? It seems like it should be correct because if the greater momentum of stream 1 pushes the stream identified as $m_f$ up, then it seems like it should do the same to the stream identified as $m_b$.

 

[Lnewqban]

After thinking about it, I don't think the above required.

All is required to have energy conserved is that each stream is split in two parts, each part is then deflected without speed loss and recombines with one of the parts of the other intial stream that is deflected in the same direction.

But the OP reads "After the collision, liquid flows in two different directions".

Could you please extend your explanation?

It seems to me that both initial velocities can't become final ones of different value which could coexist in the same stream.

 

[rdemyan]

But the OP reads "After the collision, liquid flows in two different directions".

Could you please extend your explanation?

It seems to me that both initial velocities can't become final ones of different value which could coexist in the same stream.

Please confirm that by initial velocities you are referring to the velocities of the split streams after the collision, specifically to $v_1$ and $v_2$. If so, then you are quite right; these different velocities will not coexist in the combined stream identified as $m_f$ and as $m_b$. I only used the splitting technique to determine $m_b$ (via $m_{b1}, m_{b2}$) and $m_f$ (via $m_{f1}, m_{f2}$). Because $v_1 = u_1$ and $v_2 = u_2$ due to no energy loss assumption, these split stream velocities disappear from the calculations for $m_b$ and $m_f$. The velocity, $v$, which is the velocity for the total forward stream and total backward stream, was calculated from an overall momentum balance. I did not try to determine $v$ from a calculation involving $v_1$ and $v_2$; for example by some type of mass flowrate weighted calculation.

I would very much appreciate your input on the accuracy of the diagram in the original post. I'm thinking that the diagram should probably be the second diagram (assuming the momentum of incoming stream 1 is greater than the momentum of incoming stream 2) in my first reply post.

 

[jbriggs444]

After thinking about it, I don't think the above required.

All is required to have energy conserved is that each stream is split in two parts, each part is then deflected without speed loss and recombines with one of the parts of the other intial stream that is deflected in the same direction.

So you have, for example, a stream of milk proceeding at 45 degrees up and to the right. Impinging on this is a stream of water proceeding at 45 degrees up and to the left.

The result after the interaction is a mixed stream of 50% milk and 50% water proceeding at 45 degrees up and to the right and a second mixed stream of 50% water and 50% milk proceeding at 45 degrees up and to the left.

Sure, that conserves both momentum and energy. That particular interaction is just 50% "elastic bounce" and 50% "don't interact".

More generally, one could have an interactor-a-tron which collects the two streams, harvests their kinetic energy (relative to the CoM) and spits out two or more new streams with zero total momentum (relative to the CoM) and the requisite total kinetic energy (relative to the CoM).

 

[Lnewqban]

Please confirm that by initial velocities you are referring to the velocities of the split streams after the collision, specifically to $v_1$ and $v_2$.

No, I am calling u₁ and u₂ shown in the OP diagram initial (or pre-impinging) velocities.

This is an interesting problem, which practical case I have never seen.
That is my reason to ask questions here, besides the lack of cause-effect I see for the direction of the final velocities v to be along a horizontal line, as represented in the diagram.

I am also thinking about factors affecting the outcome, like mixability of both fluids and viscosity and density of each.

 

[rdemyan]

No, I am calling u₁ and u₂ shown in the OP diagram initial (or pre-impinging) velocities.

This is an interesting problem, which practical case I have never seen.
That is my reason to ask questions here, besides the lack of cause-effect I see for the direction of the final velocities v to be along a horizontal line, as represented in the diagram.

I am also thinking about factors affecting the outcome, like mixability of both fluids and viscosity and density of each.

A practical application would be two liquid jets impinging upon one another. When the jets are equal (i.e. $m_1 = m_2 = m$ and $u_1 = u_2 = u$), most researchers assume that the velocity of the liquid sheet, which forms from the stagnation point in the impingement zone, is equal to the jet velocity, $u$ (for now assume that the velocity profile in each jet is flat or uniform). This would be the case, I believe, where no energy is given up as a result of the collision, i.e. 100% elastic. My question would apply to cases where the momentum of the jets or streams is different. I'm thinking that the major question here is what happens to that backward stream (forward and backward streams are produced because of the stagnation point in the impingement zone). I really now think that the drawing should be as shown in the second drawing of my first reply post. I've asked several responders if they agree, but as of yet no response on that particular question.

 

[Lnewqban]

My question would apply to cases where the momentum of the jets or streams is different.

According to this article that I have found, that introduces an additional complication to a seemly complicated phenomenon of the water sheet formation and breakup.

https://onlinelibrary.wiley.com/doi/10.1155/2019/9514848

 

[A.T.]

So you have, for example, a stream of milk proceeding at 45 degrees up and to the right. Impinging on this is a stream of water proceeding at 45 degrees up and to the left.

The result after the interaction is a mixed stream of 50% milk and 50% water proceeding at 45 degrees up and to the right and a second mixed stream of 50% water and 50% milk proceeding at 45 degrees up and to the left.

Sure, that conserves both momentum and energy. That particular interaction is just 50% "elastic bounce" and 50% "don't interact".

Yes, but closer to the OPs example would be: A larger fraction of each stream is deflected to exactly up, while a smaller fraction is deflected to exactly down. So you end up with two opposed streams.

More generally, one could have an interactor-a-tron which collects the two streams, harvests their kinetic energy (relative to the CoM) and spits out two or more new streams with zero total momentum (relative to the CoM) and the requisite total kinetic energy (relative to the CoM).

Yes, in general there seem to be many solutions that satisfy the conditions above.

One constraint colud be: Partial outgoing streams that are going in the same direction and thus are being combined need to have equal speeds. Otherwise the mixing to a stream of uniform speed would not conserve energy.

 

[rdemyan]

Yes, but closer to the OPs example would be: A larger fraction of each stream is deflected to exactly up, while a smaller fraction is deflected to exactly down. So you end up with two opposed streams.

Yes, in general there seem to be many solutions that satisfy the conditions above.

One constraint colud be: Partial outgoing streams that are going in the same direction and thus are being combined need to have equal speeds. Otherwise the mixing to a stream of uniform speed would not conserve energy.

Hmm... Not sure why the split streams of my "model" would have to have the same speed in order to be able to hypothetically "mix" them in order to conserve energy. The splitting is just a way to determine $m_{b1},m_{b2},m_{f1},m_{f2}$. Once the outgoing flows are known, then I think I should be able to use Eq. 12 in the original post to calculate $v$. Further, when calculating the split amounts it was assumed that the two split stream velocities for each incoming stream (1 or 2) were equal to that incoming stream velocity. However, I still can't get $v$ calculated from equation 12 to equal that calculated from an energy balance for the case where no energy is dissipated as a result of the collision. Also, based on some comments it seems like setting $v_1$ and $v_2$ equal to $u_1$ and $u_2$, respectively, might not be enough to guarantee a 100% elastic collision. The directions of the outgoing streams as well as the angles of deflection have to be correct.

With regards to the diagrams I have posted, only the diagram of the original post provides realistic calculations for a wide variety of momentum differences between the two incoming streams. Also, it is the only diagram that provides realistic calculations when I insert my theory on how to handle cases where energy is dissipated as a result of the collision. By realistic calculations I mean primarily that the calculated mass flow rate in the backward direction ($m_b$) is never negative. If it were negative, it leads to calculated mass flow rates in the forward direction ($m_f$) that exceed the combined mass flowrates of the incoming streams (which is not possible.). Further any conceptual diagram must result in equations where the calculation of the deflection angle ($\alpha$) must be no greater than $\beta$ and only approaches $\beta$ when one incoming stream has a momentum that is much greater than the momentum of the other incoming stream.

 

[erobz]

Why are you working with solid mechanics instead of continuum. If a ball collides with another ball you don't get one of the balls sometimes going one way and sometimes the other under the same conditions (as your diagram suggests for the continuum mechanics).

If the jets imping and mass ,momentum, and energy are conserved in the control volume then the result should be like this IMO:

 

[A.T.]

Hmm... Not sure why the split streams of my "model" would have to have the same speed in order to be able to hypothetically "mix" them in order to conserve energy.

If you want to mix two streams going in the same direction but at different speeds, to get a single stream moving at one uniform speed (no speed variation within the final stream), then you effectively have a completely inelastic collision during the mixing and speed homogenisation.

Like when a faster clay ball catches up to slower one, and they end up stuck to each other, moving at the same speed.

Macroscopic kinetic energy is not conserved in those cases.

 

[rdemyan]

I think I see where the problem is. In my original post, I assumed that the the stream $m_f$ and the stream $m_b$ have both the same velocity, $v$, as well as the same angle of deflection, $\alpha$. After watching some videos on ball collisions, this is likely not the case. I think I can assume that the velocities are the same but not the angles of deflection.

 

[rdemyan]

Why are you working with solid mechanics instead of continuum. If a ball collides with another ball you don't get one of the balls sometimes going one way and sometimes the other under the same conditions (as your diagram suggests for the continuum mechanics).

If the jets imping and mass ,momentum, and energy are conserved in the control volume then the result should be like this IMO:

View attachment 359244

This is not correct if the collision is elastic. The paper by Hasson and Peck from 1964 for impinging streams which are jets that have uniform velocities (throughout the jets) clearly illustrates that there is flow in the backward direction. This is physically observed in experiments with impinging jets. However, their paper assumes equal incoming streams and therefore there is no deflection angle relative to the x axis. Further, they assume that the velocity for both the forward and backward outgoing streams is the same.

If you look at the diagram, it is the stagnation point which results in flow in the forward and backward directions (flow is diverted around the stagnation point). The quantities of each flow can be determined if the separation stream line is known.
See the attached diagram.

 

[A.T.]

The paper by Hasson and Peck from 1964 for impinging streams which are jets that have uniform velocities, throughout the jets, clearly illustrates that there is flow in the backward direction. This is physically observed in experiments with impinging jets. However, their paper assumes equal incoming streams and therefore there is no deflection angle relative to the x axis. Further, they assume that the velocity for both the forward and backward outgoing streams is the same.
See the attached diagram.

Yes, that's exactly what I envisioned in post #13.

 

[rdemyan]

Yes, that's exactly what I envisioned in post #13.

Yes. If I assume that, now with unequal impinging streams, the velocities of the forward and backward stream are equal but the deflection angles are different, I am left with 5 unknowns ($m_f, m_b, v, \alpha, \phi$) where $\alpha$ is the deflection angle for the forward outgoing stream and $\phi$ is the deflection angle for the backward outgoing stream. There are four equations: x momentum balance, y momentum balance, mass balance and energy balance. For a perfectly elastic collision, $v$ can be immediately calculated from the energy balance which is Eq. 14 in my original post. But that still leaves 4 unknowns and 3 equations. Is there perhaps another equation I am missing?

 

[erobz]

Well, lets say in the event of the back stream is negligibly small, none of this would be possible without viscous effects. So its naive to say that energy and momentum is conserved for mating jets in general?

I see in the diagram, that the jet decrease in cross-sectional area. Is that observed?

 

[erobz]

I came up with a “solution” conserving mass, momentum, energy and it “looks”like it’s consistent with my diagram, but it’s probably flawed. I have to check some values though.

 

[rdemyan]

Well, lets say in the event of the back stream is negligibly small, none of this would be possible without viscous effects. So its naive to say that energy and momentum is conserved for mating jets in general?

I see in the diagram, that the jet decrease in correctional area. Is that observed?

When liquid jets collide (assuming perfect on-axis impingement) a thin liquid sheet is formed as shown in the sketch by Hasson and Peck. Also if you look at Post #12 there are pictures of this formed liquid sheet.

You are right that when the back stream is negligibly small, then energy is not conserved and if the incoming jets are equal then the velocity of the formed sheet is equal to the component velocity of the jets in the x-direction (i.e. $v_ocos\theta$ in the Hasson and Peck figure).

For unequal impinging streams I can readily solve all equations when $m_b$ is zero. The difficulty I am having is when $m_b$ is not equal to zero or as you state negligibly small. Look at Eq. 12 in my original post. The velocity of the outgoing streams is determined by $m_f-m_b$. The lowest value of $v$ occurs when $m_b$ is equal to zero. However, as the difference decreases, the calculated velocity $v$ increases and should reach the maximum value for $v$ if the collision is perfectly elastic. However, Eq. 12 assumes that the deflection angle is the same for both outgoing streams which is probably incorrect. Still my statement regarding the difference probably is still correct.

 

[rdemyan]

Attached is an updated diagram of the impingement of unequal streams. Here I am assuming that the velocity of the forward and backward outgoing streams is the same. However, the angles of deflection are not the same. The drawing assumes that the momentum of incoming stream #1 is greater than incoming stream #2. The deflection angle, $\alpha$, will be positive as shown, but I'm not sure about $\phi$. Maybe the backward outgoing stream will point downward instead of upward as shown in the diagram. This might well be a function of the impingement angle, $2\beta$.

I need one more equation. Probably some type of relationship between $\alpha$ and $\phi$ probably including $\beta$.

Here are the equations I currently have,

Momentum:
$$m_1u_1\cos\beta + m_2u_2\cos\beta = m_fv\cos\alpha - m_bv\cos\phi$$

$$m_1u_1\sin\beta- m_2u_2\sin\beta = m_fv\sin\alpha + m_bv\sin\phi$$

Mass:
$$m_f + m_b = m_1 + m_2$$

Energy (assuming a perfectly elastic collision):

$$v = \sqrt{\frac{m_1u_1^2 + m_2u_2^2}{m_1 + m_2}}$$

 

[rdemyan]

I used all 3 Law's ( Typical of Reynolds Transport relationships for steady flow and uniformly distributed properties) and an additional result for the dentition of the outflow density that I just surmise to be the case to satisfy just the equations that would produce a solution for two inflow one outflow.

$$ \rho_3 = \frac{\rho_1 v_1 A_1 + \rho_2 v_2 A_2}{A_3 v_3}$$

I can't see how you can constrain another outflow, I'm not even sure if what I did was kosher.

Right now I'm trying to solve a case where $\alpha + \phi$ = 90 degrees. This happens for billiard balls when the masses of each ball are the same and if the collision is perfectly elastic. So, I am setting $m_1 = m_2$. with $u_1 > u_2$. Then I'm guessing $\alpha$ and calculating $m_b$ from both the x momentum balance and y momentum balance. $\alpha$ is adjusted until the calculations for $m_b$ from the two momentum balances are the same. Seems like this should apply to the system I'm working on. But, at the moment kind of strange results and I need to check for errors.

 

[erobz]

Right now I'm trying to solve a case where $\alpha + \phi$ = 90 degrees. This happens for billiard balls when the masses of each ball are the same and if the collision is perfectly elastic. So, I am setting $m_1 = m_2$. with $u_1 > u_2$. Then I'm guessing $\alpha$ and calculating $m_b$ from both the x momentum balance and y momentum balance. $\alpha$ is adjusted until the calculations for $m_b$ from the two momentum balances are the same. Seems like this should apply to the system I'm working on. But, at the moment kind of strange results and I need to check for errors.

I guess I don't understand something. With a billiard ball model, $m_f,m_b$ must be equal to $m_1,m_2$ in some order. Are you allowing the billiard balls to break, while undergoing elastic collision?

 

[rdemyan]

I guess I don't understand something. With a billiard ball model, $m_f,m_b$ must be equal to $m_1,m_2$ in some order. Are you allowing the billiard balls to break, while undergoing elastic collision?

I'm not sure what I'm doing is correct at all. I'm just trying to see if somehow I can get something to work. No, I'm not allowing them to break. $m_f + m_b = m_1 + m_2$ is true and for this specific case $m_1 = m_2$. But if the assumption that the angles sum to 90 degrees requires that $m_b = m_1=m_2$, then this won't work. I am getting results where this is not the case, but the angles seem weird. For example, if $u_1$ is 1000 times greater than $u_2$, shouldn't the deflection as measured from the x-axis be pretty close to the incoming half angle of $\beta$ because sheet 2 isn't able to deflect sheet 1 much due to the much much lower momentum. But I'm only calculating a deflection of about 8 degrees for $\alpha$ but 82 degrees for $\phi$.

EDIT: Actually, I think I have this wrong with regards to deflection. If the ratio of velocities is 5, then $\alpha$ is equal to 2.1 degrees which is large deflection of the greater momentum stream. If the ratio of velocities is 1000, then $\alpha$ is equal to about 8 degrees, which is less deflection, which seems correct but also seems very low.

 

[erobz]

Right now I'm trying to solve a case where $\alpha + \phi$ = 90 degrees. This happens for billiard balls when the masses of each ball are the same and if the collision is perfectly elastic.

Can you prove that from the Conservation of Momentum and Energy?

$$ \mathbf{v_1} +\mathbf{v_2} = \mathbf{v'_1} +\mathbf{v'_2} $$

$$ \mathbf{v_1}^2 +\mathbf{v_2}^2 = \mathbf{v'_1}^2 +\mathbf{v'_2}^2 $$

Because I believe that is true if one of the particles is initially at rest, but it doesn't seem it would be the case in general.

 

[rdemyan]

Can you prove that from the Conservation of Momentum and Energy?

$$ \mathbf{v_1} +\mathbf{v_2} = \mathbf{v'_1} +\mathbf{v'_2} $$

$$ \mathbf{v_1}^2 +\mathbf{v_2}^2 = \mathbf{v'_1}^2 +\mathbf{v'_2}^2 $$

Because I believe that is true if one of the particles is initially at rest, but it doesn't seem it would be the case in general.

I've given up on this and you are most likely right that it only works if one of the particles is initially at rest.

 

[A.T.]

I've given up on this and you are most likely right that it only works if one of the particles is initially at rest.

You can always transform into a reference frame, where the fluid in one of the incoming streams is initially at rest, while the fluid in the other stream initially moves along one axis only. Then you solve the (potentially simpler) problem there, and transform the resulting outgoing velocities back to the original frame.

Just don't confuse the direction of the velocity of the fluid in a stream with the orientation of the stream. They are parallel in your original frame, but not necessarily in other frames.

 

[rdemyan]

You can always transform into a reference frame, where the fluid in one of the incoming streams is initially at rest, while the fluid in the other stream initially moves along one axis only. Then you solve the (potentially simpler) problem there, and transform the resulting outgoing velocities back to the original frame.

Just don't confuse the direction of the velocity of the fluid in a stream with the orientation of the stream. They are parallel in your original frame, but not necessarily in other frames.

I'm going to try to switch to the zero momentum frame of reference. Should I start a new thread as I am definitely going to need help?