Calculate Velocity Ratio for Inelastic Collisions

[senseandsanity]

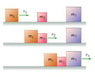
Mass 1 is moving with an initial speed of v_1, which undergoes a completely inelastic collision with a stationary block mass 2. The two blocks then stick together and move at a speed v_2. The two blocks then collide inelastically with a third block mass 3. Assuming that the blocks slide without friction what is v_2/v_1: the ratio of the velocity v_2 of the two block system after the first collision, to the velocity v_1 of the mass 1 before the collision?

I started with 1/2(m_1)(v_1)^2=1/2*(m_1+m_2)(v_2)^2 and then solved for v_2/v_1 but I'm not sure that is the right equation. Any help would be great.

 

[Doc Al]

Use conservation of momentum, not energy.

 

[wais]

To calculate the velocity ratio for inelastic collisions, we can use the equation for conservation of momentum, which states that the total momentum before the collision is equal to the total momentum after the collision.

In this scenario, the initial momentum before the first collision is given by m1v1, since mass 1 is the only block in motion. After the collision, the two blocks stick together and have a combined mass of m1 + m2, so their total momentum is (m1 + m2)v2.

Therefore, we can set up the equation m1v1 = (m1 + m2)v2, and solve for v2/v1:

v2/v1 = m1/(m1 + m2)

This means that the velocity ratio v2/v1 is equal to the ratio of the initial mass of mass 1 to the combined mass of the two blocks after the collision. This ratio will remain the same for all subsequent collisions in the scenario given.

So in summary, to calculate the velocity ratio for inelastic collisions, we use the equation m1v1 = (m1 + m2)v2 and solve for v2/v1. In this scenario, the ratio is m1/(m1 + m2).