Calculate Volume of Solid of Revolution for y=sinx to y=cosx around y=2

[MarkFL]

Here is the question:

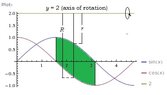
Volume obtained by rotating the region between y=sinx and y=cosx from x=pi/2 to x=pi around the line y=2?


Find the Volume obtained by rotating the region between y=sinx and y=cosx from x=pi/2 to x=pi around the line y=2.

I'm so confused about the y= 2 part, and help would be greatly appreciated!

Hint: Cos(x)^2-sin(x)^2=cos(2x)

I have posted a link there to this thread to the OP can view my work.

 

[MarkFL]

Re: Brittney Mitchell's question at Yahoo! Answers: computing the volume of a sold of revolution

Hello Brittney Mitchell,

For problems of this nature, it is always a good idea to diagram the region to be revolved along with the axis of rotation so we can see what is involved. Please refer to the following sketch:

View attachment 1891

We can see that the washer method will work best for us here since both radii are defined as one function over the given domain. So, let's begin by stated the volume of an arbitrary washer:

\(\displaystyle dV=\pi\left(R^2-r^2 \right)\,dx\)

Now, the outer radius $R$ is the distance from the axis of rotation to the bottom curve which is $\cos(x)$, hence:

\(\displaystyle R=2-\cos(x)\)

And, the inner radius $r$ is the distance from the axis of rotation to the top curve which is $\sin(x)$, hence:

\(\displaystyle r=2-\sin(x)\)

And so we may write:

\(\displaystyle R^2-r^2=\left(2-\cos(x) \right)^2-\left(2-\sin(x) \right)^2\)

Using the difference of squares formula, we may state:

\(\displaystyle R^2-r^2=\left(4-\left(\sin(x)+\cos(x) \right) \right)\left(\sin(x)-\cos(x) \right)\)

Distributing, we obtain:

\(\displaystyle R^2-r^2=4\left(\sin(x)-\cos(x) \right)+\left(\cos^2(x)-\sin^2(x) \right)\)

And using a double-angle identity for cosine (the provided hint), we obtain:

\(\displaystyle R^2-r^2=4\left(\sin(x)-\cos(x) \right)+\cos(2x)\)

Thus, the volume of the arbitrary washer may be given as:

\(\displaystyle dV=\pi\left(4\left(\sin(x)-\cos(x) \right)+\cos(2x) \right)\,dx\)

And, summing up all the washers to get the volume of the described solid of revolution, we obtain:

\(\displaystyle V=\int_{\frac{\pi}{2}}^{\pi} 4\left(\sin(x)-\cos(x) \right)+\cos(2x)\,dx\)

Applying the FTOC, we get:

\(\displaystyle V=\pi\left[-4\left(\cos(x)+\sin(x) \right)-\frac{1}{2}\sin(2x) \right]_{\frac{\pi}{2}}^{\pi}\)

\(\displaystyle V=-\pi\left(\left(4((-1)+0)+0 \right)-\left(4(0+1)+0 \right) \right)=-\pi(-8)=8\pi\)

Thus, we find the volume of the solid in units cubed is $8\pi$.