ddobre
- 33
- 2
Homework Statement
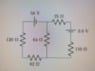
The circuit above has five resistors. Calculate the current through each.
Homework Equations
I1 = I2 + I3 (Node Law)
∑Vi = 0 (Loop Law)
The Attempt at a Solution
I tried to equate the currents using the node law, with I3 = I1+I2+I4+I5
But I see a flaw here, because the currents seem to oppose each other at the node. Anyway, I tried to solve a system of equations using the above relation of currents, and seemed to get nowhere. Any advice?