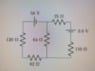
Homework Help Overview
The discussion revolves around a circuit with five resistors and two batteries, focusing on calculating the current through each resistor using circuit laws.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss applying Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL) to establish relationships between the currents. There is an exploration of the correct equations to use, with some questioning the assumptions made about current directions at the nodes.
Discussion Status
Participants are actively engaging with the problem, offering corrections to equations and discussing the implications of current direction. Some guidance has been provided regarding the number of equations needed to solve for the currents, but no consensus has been reached on a final approach.
Contextual Notes
There is mention of potential sign errors and the importance of defining current directions clearly. The discussion also highlights the need for a system of equations to solve for the unknown currents.