Calculating ΔS and P(final) for a Diatomic Ideal Gas in a Partitioned System

  • Thread starter Thread starter Noman Rasheed
  • Start date Start date
Click For Summary

Homework Help Overview

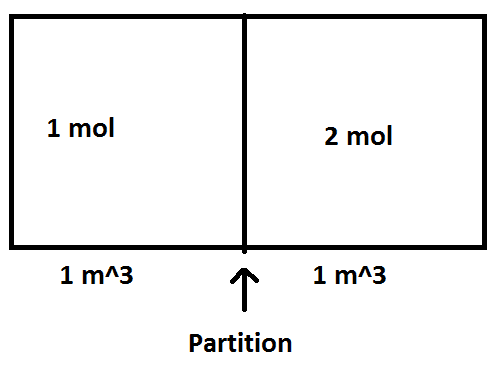
The discussion revolves around a problem involving a diatomic ideal gas (N2) in a partitioned system. Participants are tasked with calculating the change in entropy (ΔS) and the final pressure (P_final) of the gas. The initial conditions include a volume of 1 m³ for each block, a molar mass of 28 g/mol, and an initial temperature of 300 K.

Discussion Character

  • Exploratory, Assumption checking, Conceptual clarification

Approaches and Questions Raised

  • Participants discuss the application of the ideal gas law to find initial pressures and consider the implications of the first law of thermodynamics on internal energy and temperature. There are inquiries about how to connect internal energy changes to final temperature and the work done by the gases.

Discussion Status

The conversation is ongoing, with participants expressing confusion about the relationships between pressure, volume, and work done in the context of a rigid container. Some have suggested using specific formulas but are uncertain about the values to apply. There is a recognition that the work done may be zero due to constant volume, but further clarification is sought regarding the heat transfer and internal energy changes.

Contextual Notes

Participants are considering the constraints of the system, including whether the partition is movable or insulated, which affects heat transfer and work calculations. There is also mention of the need for specific values (like K) to proceed with calculations.

Noman Rasheed
Messages
29
Reaction score
1
So, there is a problem given, where diatomic ideal gas N2 is involved. Both blocks have same volume: 1m3. The molar mass of gas is: 28 g/mol. Initial temperature is 300K.
H6v1yqJ.png


I need to find ΔS and PF.

First, I did find P1 by using formula: PV = nRT
so, P1 = 1*8.3145*300/1 = 2494.35 Pa
and P2 = 2*8.3145*300/1 = 4988.7 Pa

Finally: I have total moles = 3, and total V = 2 m3.
What should I consider next?
 

Attachments

  • H6v1yqJ.png
    H6v1yqJ.png
    1.7 KB · Views: 929
Physics news on Phys.org
Noman Rasheed said:
So, there is a problem given, where diatomic ideal gas N2 is involved. Both blocks have same volume: 1m3. The molar mass of gas is: 28 g/mol. Initial temperature is 300K.
View attachment 216245

I need to find ΔS and PF.

First, I did find P1 by using formula: PV = nRT
so, P1 = 1*8.3145*300/1 = 2494.35 Pa
and P2 = 2*8.3145*300/1 = 4988.7 Pa

Finally: I have total moles = 3, and total V = 2 m3.
What should I consider next?
What does the first law of thermodynamics tell you about the change in internal energy of this system? Based on that, what is the final temperature of the system?
 
Chestermiller said:
What does the first law of thermodynamics tell you about the change in internal energy of this system? Based on that, what is the final temperature of the system?
The first law of the thermodynamics says that the change in internal energy = heat added to the system - work done by the system.
However, I can't connect the dots with the final temperature based on this definition. Any hints please?
 
Noman Rasheed said:
The first law of the thermodynamics says that the change in internal energy = heat added to the system - work done by the system.
However, I can't connect the dots with the final temperature based on this definition. Any hints please?
As I said, in this particular problem, what is the total change in internal energy of the system comprised of the two gases? How much heat is added to the system? How much work do the gases do on their rigid container?
 
Chestermiller said:
As I said, in this particular problem, what is the total change in internal energy of the system comprised of the two gases? How much heat is added to the system? How much work do the gases do on their rigid container?

I am so confused right now.
I have the value of ϒ, which is 1.4. I can also use formula: pVϒ = K, but I don't know which p should I use. As, I come up with values for pressure. Further, work done could be found out by K(Vf1-ϒ - Vi1-ϒ)/(1-ϒ). Still I don't know how to find the value of K.
 
Noman Rasheed said:
I am so confused right now.
I have the value of ϒ, which is 1.4. I can also use formula: pVϒ = K, but I don't know which p should I use. As, I come up with values for pressure. Further, work done could be found out by K(Vf1-ϒ - Vi1-ϒ)/(1-ϒ). Still I don't know how to find the value of K.
What is the change in volume of the rigid container holding the gases? Based on this, how much work does the system comprised of the two gases do on their surroundings (I.e., on the rigid container)?
 
Chestermiller said:
What is the change in volume of the rigid container holding the gases? Based on this, how much work does the system comprised of the two gases do on their surroundings (I.e., on the rigid container)?
Volume is constant.
 
Noman Rasheed said:
Volume is constant.
And the work the gases do on the rigid container comprising their surroundings?
 
Chestermiller said:
And the work the gases do on the rigid container comprising their surroundings?
I can't find out work done, since I don't have the value of K. I can figure out K, but I just don't know whether I use p2 or p1 in the formula.
 
  • #10
Noman Rasheed said:
I can't find out work done, since I don't have the value of K. I can figure out K, but I just don't know whether I use p2 or p1 in the formula.
The gases do zero work on their surroundings (I.e., the rigid container) because, treating the container as a black box, ##\Delta V=0##. And the heat entering is also zero, since the container is insulated. So the change in internal energy= ?
 
Last edited:
  • #11
Is the partition forced to move gradually, or is it free to move on its own (unconstrained)? Is the partition insulated, so that no heat can pass from one side to the other, or is it conductive to heat?
 

Similar threads

Ideal Gas Law and Pressure at 80°C
  • · Replies 2 ·
Replies
2
Views
3K
What is the molar heat capacity of an ideal gas at constant pressure and volume?
  • · Replies 5 ·
Replies
5
Views
3K
Calculations using the Ideal Gas Law
  • · Replies 2 ·
Replies
2
Views
2K
What Is the Highest Temperature Reached in the Ideal Gas Cycle?
  • · Replies 4 ·
Replies
4
Views
3K
Minimum heat removed from gas to restore its state
  • · Replies 5 ·
Replies
5
Views
3K
Closed cycle of an ideal gas
  • · Replies 3 ·
Replies
3
Views
2K
Ideal Diatomic Gas - Final temp and pressure
  • · Replies 2 ·
Replies
2
Views
3K
Mixing two gases in an isolated system and calculating final p and T
  • · Replies 4 ·
Replies
4
Views
2K
Ideal gas - monatomic or diatomic?
  • · Replies 9 ·
Replies
9
Views
24K
Change in entropy of an ideal gas during thermodynamic cycle
  • · Replies 1 ·
Replies
1
Views
2K