aron silvester
1. The problem statement, all variables, and given/known data
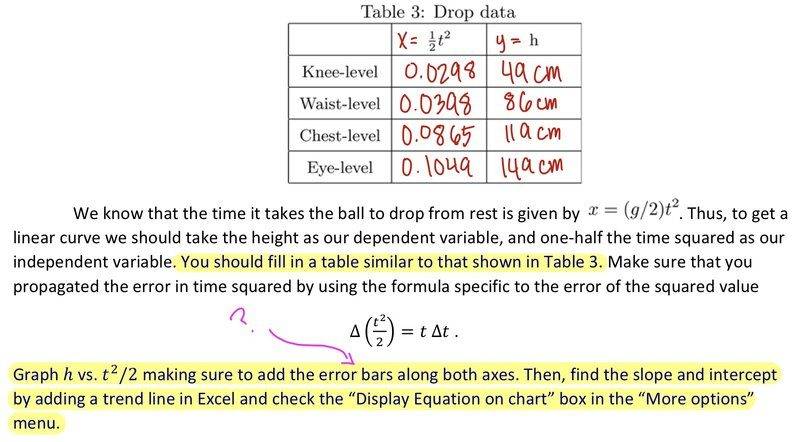

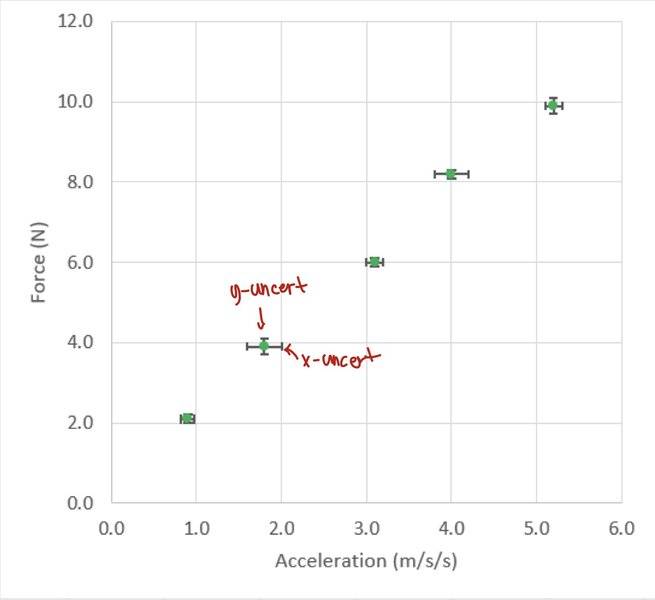
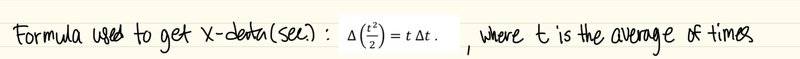 The end goal is to plot a graph on excel that looks something like the image below. I have both the X and Y values, but I just need to figure out the error bars for the X axis.
The end goal is to plot a graph on excel that looks something like the image below. I have both the X and Y values, but I just need to figure out the error bars for the X axis.
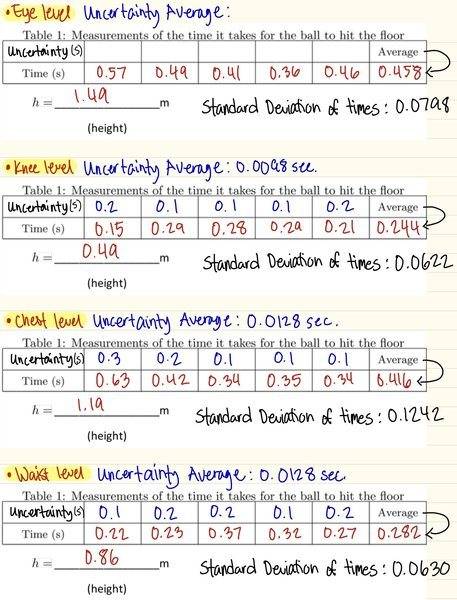
- Take the ball and drop it from chest level 5 times recording the times and the height. Do this same procedure once again for knee, waist, and eye level. You should now have four data points for your height and four data points for the time, each with uncertainty estimates. We used the average (calculated in the Collecting data section below) of the times to plug in the t variable in the X column for each level. MY QUESTION IS, HOW DO I CALCULATE THE THE ERROR BAR ALONG THE X AXIS? I already know the error bar along the Y axis (height), my group member
- Collecting data
- Data set: Similar to Table 3