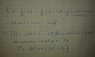Calculating generalized force in two different ways

[amjad-sh]

Homework Statement

a ladder of length L and mass m is leaning against a wall as shown in the figure below. assuming the wall and the floor are frictionless, the ladder will slide down the floor and until the left end loses contact with the wall. Before the ladder loses contact with the wall there is one degree of freedom θ.
1.Express the kinetic energy interms of θ and dθ/dt.

2.find the virtual work and the generalized force.

Homework Equations

Note: the bold symbols are related to vectors.
T=1/2 ×i=1∑i=M (mi×dsi/dt⋅dsi/dt)=T(q1,...,qn,dq1/dt,...,dqn/dt).⇒⇒⇒formula of kinetic energy. (1)
M is all parts of the system.
δw=k∑×(i∑Fi*∂ri/∂qk)δqk.⇒⇒⇒formula of virtual work. (2)
k is the number of degrees of freedom,and qk is a degree of freedom
i∑Fi*∂ri/∂qk=Fk(generalized force). (3)

Fk=d/dt(∂T/∂(dqk/dt))-∂T/∂qk.(4)

The Attempt at a Solution

[/B]I used Cartesian coordinates, the part related to the ground is the x-axis and how the ladder is high from the ground is the y axis. Let the origin be the point of contact of the ladder with the ground and "s" is how each infinitesimal part is far from the origin.

1.Let "h" be the distance between the point of contact of the ladder with the ground and the wall, let "y" the distance between the point of contact of the ladder with the wall and the ground.
The vector Si=hii+yij.
dsi/dt=dhi/dti+dyi/dtj.
h=cosθs.
y=sinθs.
si.si=(dθ/dt)2 *(sinθ)2*s2 +(dθ/dt)2*(cosθ)2*s2
(dsi/dt)2=s2 *(dθ/dt)2
T=0∫L (dT)=0∫L (1/2*dm*(ds/dt)2)=0.5*0∫L(M/L*ds*s2*(dθ/dt)2)=0.5*(dθ/dt)2*M/L*0∫Ls2*ds=1/6*(dθ/dt)2*ML2

2. I calculated here the generalized force.

∂ri/∂θ=∂h/∂θi+∂y/∂θj=-(dθ/dt)sinθsi+(dθ/dt)cosθsj

Using contious form of equation (3) we get :
Fk=(intergrate from zero to L) ∫dmgj.(-(dθ/dt)*sinθ*si +dθ/dt*cosθ*sj)
I get finally Fk=Mg(dθ/dt)*cosθ*(L/2).

when I use equation (4) to get the generalized force I get different answer, so is there something wrong in my solution?

 

[andrewkirk]

I'm afraid your post is too hard to read the way it is set out, so there is unlikely to be much help offered. I suggest you read the physicsforums LaTeX primer about how to set out formulas using LaTeX, then you'll be able to rewrite the post in a way that's easy to read, and you're likely to get much more help.

Good luck!

 

[amjad-sh]

I rewrote my question, but I used my handwriting to write my attempt to the solution.I will use Latex in my later posts.

Homework Statement

a ladder of length L and mass m is leaning against a wall as shown in the figure below. assuming the wall and the floor are frictionless, the ladder will slide down the floor and until the left end loses contact with the wall. Before the ladder loses contact with the wall there is one degree of freedom θ.
1.Express the kinetic energy interms of θ and dθ/dt.

2.find the virtual work and the generalized force.

Homework Equations

They are written in the papers uploaded below.

3. The Attempt at a Solution

I calculated the generalized forced in different ways, but unfortunately I got two different answers.
So if anybody can show to me a hint or tell me where I missed.
My attempts are written in the uploaded pictures below.
dm=M/L*ds.
I integrated from zero to L in all the integrals written.
and it is dm in the integral of page 4 not m.