Shaye
- 20
- 7
- Homework Statement
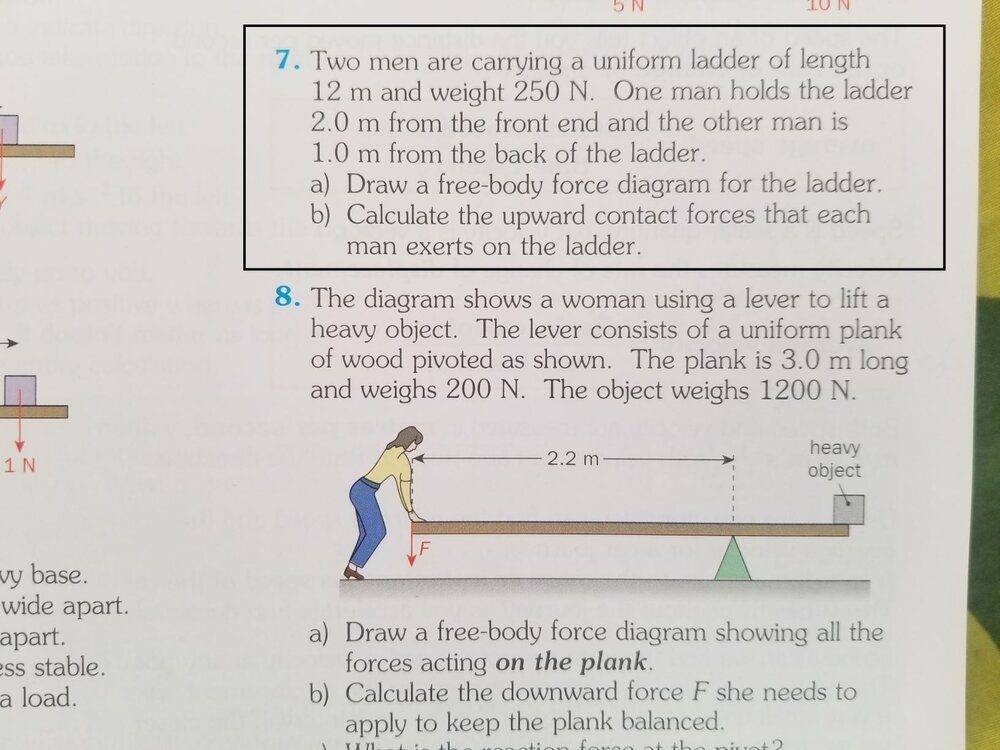
- I am required to calculate the upward contact forces that two men are exerting carrying a ladder horizontally at fixed points (question 7). I think I should calculating moments about each fixed point (where the men are carrying the ladder)
- Relevant Equations
- Moment of Force = Force * Perpendicular distance
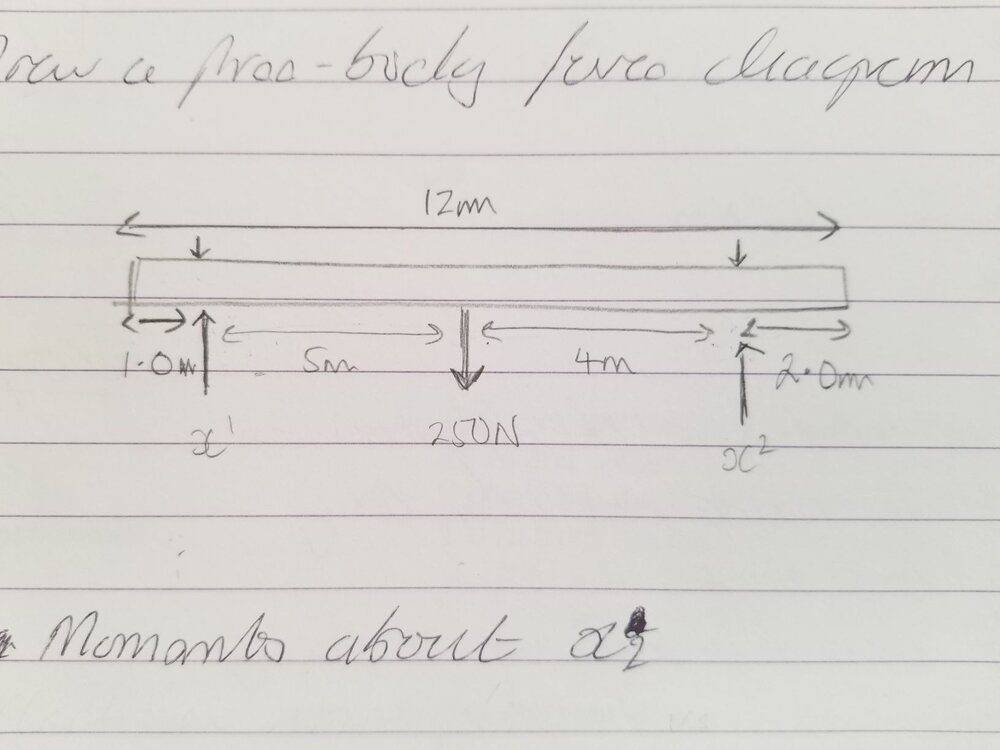
Moment about X2 to calculate force at X1:
x1 * 9 = (250 * 2)
Therefore, x1 = 500/9 = 55.5N
The book however gives force at x1 as 110N. So I figured I have not understood a concept somewhere
x1 * 9 = (250 * 2)
Therefore, x1 = 500/9 = 55.5N
The book however gives force at x1 as 110N. So I figured I have not understood a concept somewhere