Calculating peak voltage in a center-tapped transformer

[JJBladester]

Homework Statement

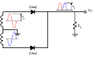
Calculate the peak voltage across each half of a center-tapped transformer used in a full-wave rectifier that has an average output of 120V.

Homework Equations

Assuming the practical model (factoring voltage drop across diodes but not the diodes' dynamic resistance)...

V_{out (avg)}=\frac{2(V_{sec}-V_{th})}{\pi }

The Attempt at a Solution

V_{out (avg)}=120V

V_{out (avg)}=\frac{2(V_{sec}-V_{th})}{\pi }

V_{sec}=\frac{(120V)(\pi )}{2}+0.7V=189.196V

The voltage across each half of the center-tapped transformer is just half of V_sec:

\frac{V_{sec}}{2}=\frac{189.196V}{2}=94.598V

My book gives an answer of 186V which makes no sense. Given: this book is known to have errata all over the place. Is this another example of a publisher error?

 

[gneill]

In a full-wave rectifier with a center-tapped transformer, each half of the secondary supplies a half-cycle at the full magnitude of the output waveform (ignoring diode drops for the moment). So, if the average value of the output voltage is 120V, that should also be the average produced by a half-secondary over the half-cycle where it supplies the output (again ignoring diode drop).

So your peak voltage for a transformer secondary half should be close to your 189V value, and twice that for the full secondary.

 

[JJBladester]

Thanks gneill. I see where I went wrong. The original formula should have V(sec) divided by 2 in parentheses inside the numerator.

Great picture, by the way.