ngn
- 20
- 1
- TL;DR
- Question about how to calculate phase shift between to sine waves from textbook. Does the book have the correct method?
Hello,
Came across this picture and passage from a textbook. Although the text lays out a method for calculating the phase shift between displacement and acceleration, I am not sure how they are calculating which wave is leading and which is lagging. From their description, it seems like a negative value would suggest that the wave is lagging compared to the reference. However, when I run the same method comparing velocity to displacement (using displacement as the reference), I get:
Displacement = 90+360+180 = 630
Velocity = 180+360+180 = 720
630 - 720 = -90
If negative means lagging, then this would suggest that velocity is lagging displacement by 90 degrees. But is that the case? It seems like the positive peaks for velocity occur earlier in time compared to the positive peaks for displacement? So, shouldn't velocity be leading displacement? Acceleration does look to be lagging displacement, so is there a problem with this method, or am I not considering the waveforms/method correctly?
Thanks!
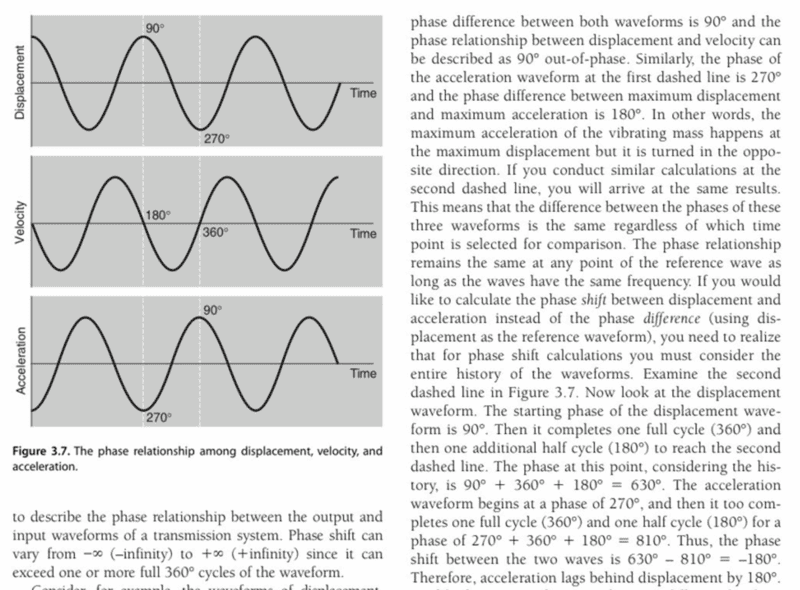
Came across this picture and passage from a textbook. Although the text lays out a method for calculating the phase shift between displacement and acceleration, I am not sure how they are calculating which wave is leading and which is lagging. From their description, it seems like a negative value would suggest that the wave is lagging compared to the reference. However, when I run the same method comparing velocity to displacement (using displacement as the reference), I get:
Displacement = 90+360+180 = 630
Velocity = 180+360+180 = 720
630 - 720 = -90
If negative means lagging, then this would suggest that velocity is lagging displacement by 90 degrees. But is that the case? It seems like the positive peaks for velocity occur earlier in time compared to the positive peaks for displacement? So, shouldn't velocity be leading displacement? Acceleration does look to be lagging displacement, so is there a problem with this method, or am I not considering the waveforms/method correctly?
Thanks!