Calculating potential energy of electric dipole in uniform field

[moderate]

This page contains one derivation for the potential energy:

http://www.shef.ac.uk/physics/teaching/phy205/lecture_4.htm"

Result: U=-pEcos$$\theta$$

where
E = magnetic field's magnitude
P = dipole moment = d*Q
d= distance between + and - charge
Q= charges' magnitude
$$\theta$$ = angle between the field and the straight line connecting the + and - charges

But, shouldn't it also be possible to derive the dipole's potential energy in another way?

The definition of electric potential energy is:

$$\Delta$$U_1->2=-W_1->2
where W=work done by electric field.

So, can't one take the 2 charges as separate (connected by a massless, chargeless rod), and then calculate the work done on them by the field while moving from the angled position to equilibrium?

This should then be equal to the initial potential energy (in the angled position).

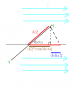
Attached is an illustration.

Calculating for the positive charge gives:

Force_electric*distance=E*q*$$\Delta$$x
Force_electric*distance=E*q*(d/2 - d/2*cos($$\theta$$)
$$\Delta$$U_q+=-E(d/2)(1-cos$$\theta$$)

Adding the changes for both charges gives:

$$\Delta$$U_0->theta=Ep(1-cos($$\theta$$)).

This gives me the same relationship, except that (which is frustrating me somewhat) there is a linear offset of (1)Ep.

My question is: the approach is valid, correct? I am not going crazy?

If that is the case, then it is just a matter of adding a linear shift to come to the same zero potential, correct?

-frustrated at physics

 

[Soph_the_Oaf]

*bump*

I derived it by integrating the torque between theta=o and theta and got the same result...

Any ideas anyone?

 

[matonski]

So, can't one take the 2 charges as separate (connected by a massless, chargeless rod), and then calculate the work done on them by the field while moving from the angled position to equilibrium?

The offset is due to the fact that you are integrating to equilibrium, which is defining U = 0 to be when p is antiparallel with the field. On the other hand, the link defines U = 0 to be where p is parallel to an equipotential and thus perpendicular to the field.