Calculating Power Dissipation in a Parallel Circuit

[Linus Pauling]

1. The 10 ohm resistor in the figure is dissipating 40W of power. How much power is the 5ohm resistor dissipating?

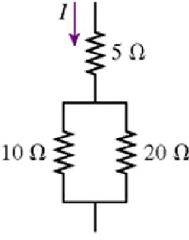
2. P = I²*R



3. I = sqrt(P/R) = 2. I then did P = I²R = (4)(5) = 20 which is incorrect.

 

[dmsgo89]

well, I have exactly same problem and I solved only one case:

So, we have 10 ohm and 40 watt.

the Power = V^2/ Ohm then we can calculate the volt on 10 ohm.


The power on 20 ohm then, is // resistor with 10 ohm.


Then they should have same potential difference.


So you can find the power at 20 ohm...



BUt...


I am lost with 5 ohm too... anybody else?

 

[GRB 080319B]

The current through the 5 ohm resistor is not equal to the current through the 10 ohm resistor, because the current "splits" at the junction where the circuit becomes parallel. Let the current through the 5 ohm resistor be I1, through 10 ohm be I2 and through 20 ohm be I3. Let the junction A be where the circuit first branches off into the 2 parallel circuits. Then, by the junction rule, the current going into junction A must be equal to the sum of the currents out of junction A and into the two parallel resistors.

Junction @ A : I1 = I2 + I3

Since P = I^2 R, we need to find I1 in order to calculate the power dissipated by the 5 ohm resistor. We use the loop rule to find current I3, since we already know I2 = 2 amps. So draw Loop 1 clockwise around the inside of the parallel part of the circuit (containing the 10 ohm and 20 ohm resistors). The sum of the voltage drops (V=IR) across the circuit equals zero. We start at the junction A, and determine the voltage drop across each resistor around the loop.

Loop 1 @ A: -(20 ohm)(I3) + (10 ohm)(I2) = 0

The Loop 1 equation gives I3 = (1/2)I2. Substituting I3 into the junction A equation, with I2 = 2 amps, we get I1 = (3/2)I2 = 3 amps. So the power dissipated by the 5 ohm resistor is P = I^2 R = (3 amps)^2 * (5 ohms) = 45 watts. Feel free to make any corrections.