Calculating Rotational Inertia and Speed of a Square Plate

Click For Summary

Homework Help Overview

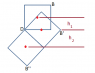
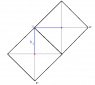
The discussion revolves around calculating the rotational inertia and speed of a uniform square plate pivoted at one vertex. The plate has a mass of 0.8 kg and a side length of 0.8 m, and it swings downward under the influence of gravity, with resistive forces neglected. Participants are tasked with finding the rotational inertia relative to the pivot point, the angular speed when a specific side is horizontal, and the linear speeds at different positions during the swing.

Discussion Character

  • Mixed

Approaches and Questions Raised

  • Participants discuss the use of the parallel axis theorem to calculate the moment of inertia and question the distances involved in the calculations. There are attempts to clarify the height changes of the center of mass during the swing and how these affect the energy conservation equations.

Discussion Status

The discussion is active, with participants exploring various interpretations of the problem setup and calculations. Some guidance has been provided regarding the use of energy conservation principles, and there is an ongoing examination of the values used for height and inertia. Participants are encouraged to clarify their reasoning and assumptions as they progress through the problem.

Contextual Notes

There is some confusion regarding the dimensions of the square plate, specifically whether the side length is 0.8 m or 1.2 m, which impacts the calculations. Participants are also discussing the correct interpretation of the height changes as the plate swings, which is critical for applying energy conservation correctly.

  • #31
From 1 to 2 I found that the center of mass move downs by .4.
From 2 to 3 I found that the center of mass move down by .4+ sqrt(2)/2*.8.
 
Physics news on Phys.org
  • #32
postfan said:
From 1 to 2 I found that the center of mass move downs by .4.
From 2 to 3 I found that the center of mass move down by .4+ sqrt(2)/2*.8.

I agree that h1 = .4 for the first part. I don't agree that h2 = .4+ sqrt(2)/2*.8 for the additional distance from question 2 to question 4.
 

Attachments

  • plate.png
    plate.png
    3.2 KB · Views: 467
  • #33
Does h2 = .8+ sqrt(2)/2*.8
 
  • #34
postfan said:
Does h2 = .8+ sqrt(2)/2*.8

No. See the attached diagram. As corner B moves from B' to B'', the center of mass moves downward a distance h2. You can see that h2 is half the diagonal of the square.
 

Attachments

  • Plate 3.png
    Plate 3.png
    3.7 KB · Views: 459
  • #35
Ok so for part 4 h= sqrt(2)/2*.8, right?
 
  • #36
postfan said:
Ok so for part 4 h= sqrt(2)/2*.8, right?

That represents the correct value of h2. What is the total h in going from where the plate is released from rest to where B is at the bottom?
 
  • #37
The total h is equal to .4+sqrt(2)/2*.8.
 
  • #38
Yes, that's right.
 
  • #39
Ok then we use the equation mgh=.5mv^2+.5Iw*2, substitute values convert angular velocity to linear velocity and then solve for v, right?
 
  • #40
Yes. [EDIT: NO]
 
  • #41
Sorry, it's late here and I'm half asleep! The total kinetic energy is just (1/2)Iw2 (as you had in post #14). So,
mgh = (1/2)Iw2.
 
  • #42
Why is that so? The question is asking for the linear speed of B.
 
  • #43
The plate is in pure rotation about D. So, as long as you use the moment of inertia about D, the kinetic energy can be expressed as just rotational KE about D.

Equivalently, you could express the kinetic energy as kinetic energy due to translation of the center of mass plus kinetic energy of rotation about the center of mass:

KE = (1/2)mVcm2 + (1/2)Icmω2. Here you would use the moment of inertia about the center of mass rather than about point D.

Either way will yield the same answer.

Once you find ω you can then find the linear speed of B.
 
  • #44
I got the answer, but I am still confused about when/how I can just use (1/2)Iw2 instead of the full (1/2)mV^2 + (1/2)Iω^2. I know it is rather late, so would you rather want to talk about it tomorrow?
 
  • #45
As I said before, you can use either KE = (1/2)IDω2 or KE = (1/2)mVcm2 + (1/2)Icmω2. Both are correct.

In this problem, the first question was to find ID. So, it will be easier to use KE = (1/2)IDω2 when setting up mgh = KE. You can then solve for ω. Then use ω to find VB.

It is late here (about 1 am) and I do need my beauty rest. So I will quit for now and check back tomorrow. :zzz:
 
  • #46
Alright, thanks for all your help! You're awesome!
 
  • #47
TSny,How did you draw the diagrams?
 
  • #48
I used Microsoft Paint.
 
  • #49
How did you get the square to rotate?
 
  • #50
In some cases I just redrew it in a rotated position. Sometimes I copy a drawing that I drew in Paint into another program that will allow me to easily rotate the figure and then copy the rotated figure back into Paint.

For example, Powerpoint allows you to easily rotate a figure any amount you want.
 
  • #51
Oh, I see.
 

Similar threads

Rotational inertia of square about axis perpendicular to its plane
  • · Replies 52 ·
2
Replies
52
Views
5K
Correct Use of the Parallel Axis Theorem for Moment of Inertia
  • · Replies 2 ·
Replies
2
Views
2K
Angular Momentum Problem: Mouse walking on a rotating turntable
  • · Replies 5 ·
Replies
5
Views
1K
Moment of inertia of a cuboid parallel to one of its faces (repost with diagram)
  • · Replies 25 ·
Replies
25
Views
2K
What is the "r" in the moment of inertia?
  • · Replies 13 ·
Replies
13
Views
3K
Moment of inertia of a rod bent into a square
  • · Replies 12 ·
Replies
12
Views
2K
Why can we use this approximation in rotational work-kinetic energy theorem for small displacements?
  • · Replies 7 ·
Replies
7
Views
1K
Moment of inertia of a metal plate about three points
  • · Replies 6 ·
Replies
6
Views
1K
Moment of inertia of T bar about 3 axes
  • · Replies 21 ·
Replies
21
Views
3K
Calculating Moment of Inertia for a Rotating Cylinder | Physics Tutorial
  • · Replies 2 ·
Replies
2
Views
2K